When considering a weak decay interaction such as leptons , the weak force is mediate by huge particle such as bosons (W+ or W- ). How it is possible to have a such heavy particle within less massive decay structure. Also what will happen to that huge mass after decay is completed. Is it simply vanishes?
Asked
Active
Viewed 623 times
2 Answers
7
When e.g. a neutron decays, there is no "real" W-boson inside, in the sense that it could be detected at every point.
Instead, the decay of the neutron involves a "virtual" W-boson, a W-boson that only exists for a very short time. Quantum mechanics allows the energy conservation law to be violated by $\Delta E$ for a very short time $\Delta t$ as long as $\Delta E \cdot \Delta t\leq \hbar/2$ or so. It means that for a very short time, the neutron may turn into a proton and a negative W-boson, although the energy conservation law seems to be violated. However, the W-boson is obliged to change into light electron and antineutrino very quickly and restore the original value of the energy.
What is actually going on requires one to use the axioms and formalism of quantum field theory. The virtual W-boson is then represented by a "propagator", an internal line in a Feynman diagram.
Luboš Motl
- 182,599
5
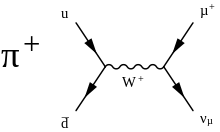
To add to the other answer: Your intuition is right in a way. The fact that the $W$ and $Z$ bosons are so heavy is the reason for the weakness of the interaction. For example, $\pi^+$ mesons can decay over the weak interaction, the process is described by the following Feynman diagram:
According to the Feynman rules, the probability amplitude of such a decay happening is proportional to $$ \mathcal{M} \sim \frac{2\textrm{i}\,g^2}{k_\mu k^\mu - M_W^2} \;, $$ where $g$ is the weak coupling constant and $k^\mu$ the $4$-momentum of the pion.
You see that there always is a probability for that to happen - because the $W$ is only "virtual" and the uncertainty relation. But that probability is suppressed by the high $W$ mass.
Noiralef
- 7,463