First, the Unruh and Hawking radiation aren't quite "the same thing". They have a similar origin and the Unruh radiation may be considered a flat space (large black hole) limit of the Hawking radiation.
Now, the near-horizon metric of an extremal black hole is $AdS_2\times S^2$ while for a non-extremal one, the $AdS_2$ is replaced by the Rindler space.
This $AdS_2$ (two-dimensional anti de Sitter space) has consequences. First, in the static coordinates, the proper distance of any observer from the event horizon diverges. On the Wikipedia page I linked to, the formula
$$ ds^2=-\frac{r^2}{M^2}\,dt^2+\frac{M^2}{r^2}\,dr^2+M^2\,\big(d\theta^2+\sin^2\theta\,d\phi^2 \big)$$
implies that near $r=0$ (which corresponded to the horizon $r=M=Q$ in the original coordinates), $s =\int ds$ is proportional to the integral of $M/r$, and therefore logarithmically diverges.
The metric in the displayed formula above is locally $AdS_2$ – the curvature is constant and it's a maximally symmetric space etc. – but it is only a part of the $AdS_2$ space. The coordinates we got were the so-called "Poincaré coordinate" and they only covered a part of the $AdS_2$ space, the so-called Poincaré patch.
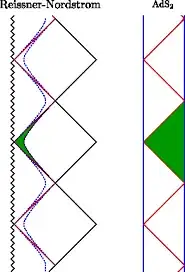
The Poincaré patch covers the green portion of the "global $AdS_2$" on the right part of the picture above. The observer sitting at the horizon however moves along the upper 45° tilted boundary of the green triangle and his trajectory inevitably is a geodesic. So he experiences no local acceleration – and no Unruh radiation. This is actually related to the fact that the near-horizon metric $AdS_2\times S^2$ with the appropriate electric or magnetic flux is a solution to Einstein's equations by itself – while the non-extremal near-horizon metric isn't a solution by itself.
Because the local curvature of these trajectories vanishes, the Unruh temperature vanishes, as also expected from the fact that when the "two horizons" coincide, the gravitational acceleration at the horizon vanishes.
So because the acceleration and temperature near this horizon is zero, there is no Unruh or Hawking radiation seen by this observer.
In the non-extremal case, there is a radiation that the observer keeping himself a bit above the horizon sees. Locally, it may be interpreted as the Unruh radiation, and the Unruh radiation could be undone in the flat space by using the non-accelerating reference frame. However, in a finite non-extremal black hole spacetime, things are different. The static Schwarzschild coordinates behave at $r=\infty$ as non-accelerating coordinate in the Minkowski space, but near $r=r_0$, they behave as the locally accelerating frame where the Unruh radiation exists. With the Schwarzschild choice of the time and the corresponding energy, we know that the fields aren't in the ground state of this Schwarzschild $H$ near $r=r_0$ because there's the Unruh radiation. Because $H$ is a symmetry of the background, it must be true after some time, too. At $r\to\infty$, these excitations must be still there, even though the curvature may already be neglected at $r\to\infty$.
So that's why the Unruh radiation is seen as a real, Hawking radiation by the observer at infinity (where the attraction by the black hole becomes negligible).
