The important quantity associated with a black hole is the event horizon area. The volume contained inside is not what one would think of as $V = 4\pi r^3/3$. More on the volume later. The important quantitiy is the area of the event horizon. The reason is that from the perspective of an exterior observer this is the limit of observation. Everything that falls into the black hole is observed to have its observed time intervals on a clock dilated or slowed as radiation it emits is red shifted arbitrarily far.
The Schwarzschild metric for a nonrotating black hole of mass $M$ gives the line element
$$
ds^2 = \left(1 - \frac{2m}{r}\right)dt^2 - \left(1 - \frac{2m}{r}\right)^{-1}dr^2 – r^2d\Omega^2~m = GM/c^2 .
$$
For null rays we have the interval is zero $ds = 0$ and we proceed to compute the clock time $t$ on a standard coordinate frame of a very distant observer for the time it takes a photon to radially escape from some distance $R$ form a black hole
$$
\int^Tdt = \int_R^\infty \left(1 - \frac{2m}{r}\right)dr = R - 2m ln(R - 2m)
$$
clearly this becomes infinite as $R \rightarrow 2m$. Physically this means that everything that made the black hole, including the original star that imploded into it are “pasted” right above the event horizon. It is as if the black hole has a geological layer cake structure of everything that went into it. Notice there is no reference at all to anything in the interior. The observer on the outside, which is the wise place to remain if you wish to keep living, witnesses everything about the black hole as pinned on the event horizon, and this is one basis for the holographic principle.
All of the stuff that composes the black hole forms the entropy of the black hole. The Bekenstein entropy for the area of a black hole event horizon
$$
S = k~\frac{A}{4\ell_{pl}^2}
$$
where the horizon area is $A = 4\pi R^2$ $= 16\pi m^2$ and $\ell_{pl} = \sqrt{G\hbar/c^3}$ is the Planck unit of length. We can see that the area of a black hole can be written according to $N$ Planck areas of a black hole, for the Planck area $A_{pl} = 4\pi\ell_{pl}^2$ and the entropy of the black hole is then given by $S = \pi k N$. From here there are all types of interesting connections with quantum information theory, but I will defer on that for now.
The interior of a black hole is only accessible to those who enter it. This is at least the case for a classical black hole. For a quantum black hole there may be some fluctuations of the horizon which make quantum information of a black hole a superposition of states outside and inside. I will not go into that for now. For the pure Schwarzschild black hole the Penrose diagram
The event horizon as seen by an observer in our universe is on the right. Once you cross the horizon it splits and the horizon separating the interior of the black hole from our universe and the other horizon separating the other universe from the interior grow apart. In this eternal black hole diagram, which is a sort of mathematical idealization, the horizons grow infinitely far apart. This means the spatial region in the interior grows, and becomes infinitely large at the singularity $r = 0$.
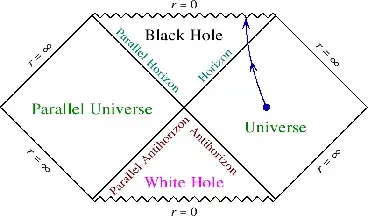
I could go further in how this mathematical idealization of the eternal black hole is perturbed by the collapsing star and by Hawking radiation. The imploding surface of a star will cut this diagram in half and the region between the material surface and the horizon will grow arbitrarily. Hawking radiation in addition cuts off the size of the distance between the collapsing surface and the horizon, or between these two split horizons. The scale of this has to do with the quantum Poincare recurrence and quantum complexity of the system, which gets us into a huge area of current research.
What is happening in the interior of a black hole is then a curiosity, and we will never know what happens in the interior of a large black hole. They are too far away, which is a good thing, and the classical nature of them makes access to the interior impossible. For quantum black holes, or more likely QCD analogus of AdS/black holes, we might be able to make inferences from quantum superposition of exterior and interior states.
