You've discovered a famous problem in thermodynamics.
In our case the piston will not move. The mechanical argument is right, while the maximum entropy argument is inconclusive.
To see that $P_1=P_2$ is an equilibrium position you can also apply conservation of energy. Since there is no heat exchange,
$$dU_{1,2} = -P_{1,2} dV_{1,2}$$
We require that $dU=0$ since our system is isolated from the environment, hence
$$dU_1 + dU_2 = 0 \to P_1 d V_1 + P_2 dV_2 = 0$$
But $V=V_1+V_2$ and $V$ is fixed, so that $dV_1 = - dV_2$ and we obtain
$$P_1=P_2$$
Now let's see the entropy maximum principle. The problem is that you forgot that $S$ is a function of energy too:
$$S(U,V)= S_1 (U_1, V_1)+ S_2 (U_2, V_2)$$
$$d S = dS_1 + dS_2 = \frac{dU_1}{T_1} + \frac{P_1}{T_1} dV_1 + \frac{dU_2}{T_2} + \frac{P_2}{T_2} dV_2$$
Since $dU_{1,2} = -P_{1,2} dV_{1,2}$, we see that $dS$ vanishes identically, so that we can say nothing about $P_{1,2}$ and $T_{1,2}$: the entropy maximum principle is thus inconclusive.
Update
Your question actually inspired me a lot of thoughts in the past days and I found out that...I was wrong.
I basically followed the argument given by Callen in his book Thermodynamics (Appendix C), but it looks like:
- There are some issues with the argument itself
- I misinterpreted the argument
My error was really silly: I only showed that $P_1=P_2$ is a necessary condition for equilibrium, not that it is a sufficient condition, i.e. (if the argument is correct and) if the system is at equilibrium, then $P_1=P_2$, but if $P_1=P_2$ the system could still be out of equilibrium...which it is!
I am still not really able to explain why the whole argument is wrong: some authors have said that equilibrium considerations should follow from the second law and not from the first and that the second law is not inconclusive.
You can read for example this article and this article. They both use only thermodynamics considerations, but I warn you that the second tries to contradict the first. So the problem, from a purely thermodynamic point of view, is really difficult to solve without making mistakes, and I have found no argument that persuaded me completely and for good.
This article takes into consideration exactly your problem and shows that the piston will move, making the additional assumption that the gases are ideal gases.
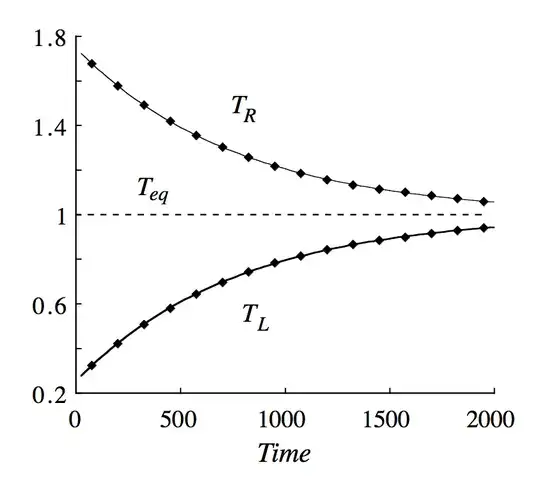
We take the initial temperatures, T1 and T2, to be different, and the initial pressures, p1 and p2, to be equal. Once unblocked, the piston gains a translational energy to the right of order 1/2KT1 from a collision with a side 1 molecule, and a translational energy to the left of order 1/2KT2 from a collision with a side 2 molecule . In this way energy passes mainly from side 2 to side 1 if T2>T1.
[...] In this process just considered, the pressures on the two sides of the piston are equal at all times, which means no "work" is done. However, the energy transfer occurs through the agency of the moving piston, and if one considers "work" to be the energy transferred via
macroscopic, non-random motion, then it appears that "work" is done.
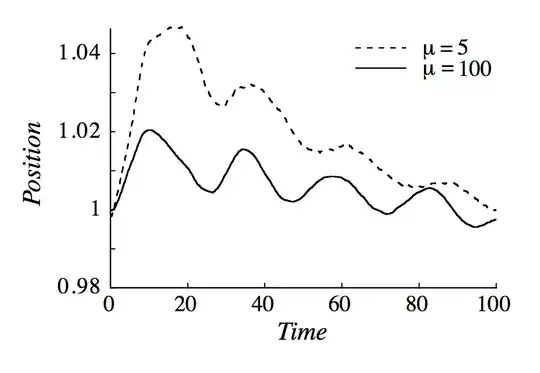
This is really similar to the argument given by Feynman in his lectures (39-4). Feynman basically uses kinetic theory arguments to show that if we start with $P_1 \neq P_2$ the piston will at first "slosh back and forth" (cit.) until $P_1 = P_2$, and then, due to random pressure fluctuations, slowly converge towards thermodynamic equilibrium ($T_1=T_2$).
The argument is really tricky because we assume that if the pressure is the same on both side the piston will not move, forgetting that pressure is just $2/3$ of the density times the average kinetic energy per particle
$$P = \frac 2 3 \rho \langle \epsilon_K \rangle$$
just like temperature is basically the average kinetic energy (without the density multiplicative factor). So we are dealing with statistical quantities, which are not "constant" from a microscopic point of view. So while thermodynamically we say that if $P_1=P_2$ the piston won't move, from a microscopic point of view it will actually slightly jiggle back and forth because of the different collision it experiences from particles in the left and right sides.
There have been also simulations of your problem which show that if we start with $P_1=P_2$ and $T_1\neq T_2$ the piston will oscillate until we reach thermodynamic equilibrium ($T_1=T_2$). See the pictures below, which I took from the article.