When talking about acoustic waves, medium continuity (pressure, density) is implicit. But can the wavelength of an acoustic wave be as small as intermolecular separation? For example, can ~10 THz sound waves travel in water?
1 Answers
I do not know how to answer your question directly. What happens at high (enough) frequencies is that the continuum model is not valid anymore. So, we can probably estimate that the maximum frequency is related to the minimum wavelength, that, is
$$\lambda_\min >> a$$
where $a$ is a characteristic scale at the micro-scale. Thus, when these two scales are far apart, we can trust the continuum model.
Below, you can see the derivation of the dispersion curves for a monoatomic crystal assuming that the interaction is with first neighbors and is mediated by linear springs. According to this model, there is a maximum limit for frequencies propagated through this material when the two length-scales are alike.
Example: Simple mass-spring lattice
Let us consider the system depicted in the following schematic
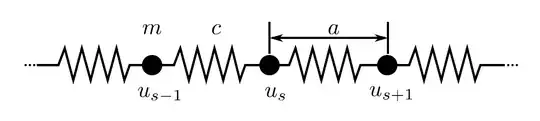
Simple mass-spring lattice.
The force in the plane $s$ cause by the displacement of the plane $s+p$ is proportional to the difference $u_{s+p}-u_s$ of the displacements. We will consider only nearest-neighbor interactions, so $p=\pm 1$. The total force on $s$ comes from planes $s=\pm 1$: \begin{equation} F_s = c(u_{s+1}-u_s)+ c(u_{s-1}-u_s). \end{equation} The constant $c$ is the stiffness between nearest-neighbor planes and will differ for longitudinal and transverse waves.
The equation of motion of the plane $s$ is $$ m \ddot{u} = c(u_{s+1} + u_{s-1} -2 u_s), $$ assuming harmonic time dependence $\exp(-i\omega t)$ \begin{equation} -m\omega^2 u_s = c(u_{s+1} + u_{s-1} - 2u_s) \enspace . \tag{1} \end{equation}
Using the Bloch theorem $$u_{s\pm 1} = u_s e^{\pm i ka}. $$ So (1) is now $$ -m \omega^2 u_s = c (u_s \exp(ika) + u_s \exp(-ika) - 2u_s) $$ and canceling $u_s$ from both sides, we have $$ \omega^2 m = -c[ \exp(ika) + \exp(-ika) - 2 ] \enspace .$$
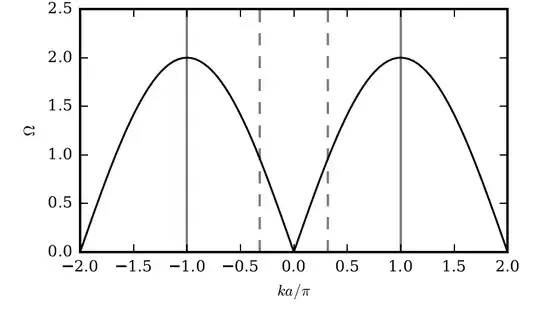
Using the identity $2\cos ka = \exp(ika) + \exp(-ika)$, and taking $\Omega^2 = \omega^2/\omega_0^2 = \omega^2 m/c$, we have the dispersion relation \begin{equation} \Omega^2 = 2 (1-\cos ka) \enspace . \tag{2} \end{equation}
The boundary of the first Brillouin zone lies at $k=\pm \pi/a$. We show from (2) that the slope of $\Omega$ versus $ka$ is zero at the zone boundary $$\frac{d\Omega^2}{d\, ka} = 2\sin ka=0$$ at $ka=\pm \pi$, $\sin ka = 0$.
By a trigonometric identity (2) may be written as \begin{equation} \Omega^2 = 4 \sin^2 \frac{1}{2}ka, \qquad \Omega = 2\left\vert \sin \frac{1}{2} ka\right\vert \enspace . \end{equation}
Plot of $\Omega$ versus $ka$. The region of $ka<<1$ or $\lambda/a>>1$ corresponds to the continuum approximation; where $\Omega$ is directly proportional to $ka$ (and is enclosed between the dashed lines). The First Brillouin Zone is placed between $-1$ and $1$.
- 1,704