How does electron makes transition from one state to another?

Question

i am not asking why it makes. i am curious about how it makes the transition. Does it go from one state to another via straight line or it makes smaller and smaller orbits till it reaches the next orbit

Answer 1

As phrased, this question suggests suggests a very Bohr-like image of electrons. This answer is intended to nudge you in the direction of a quantum model, but is by no means complete. Honestly, there's no way to understand QM without delving deep into the math, and even then its difficult to make a math <-> reality correspondence.

Firstly: quantum mechanics (QM) replaces point particles with definite momenta with a function (field) that is defined over all space and changes with time. This wave function ($\psi(\mathbf x,t)$) encodes the probability of measuring the electron at a given position, with given momentum: it evolves deterministically, but only tells you probabilistically what you might observe in a system.

Now, to answer your question: within the QM perspective, there is no notion of an orbit, or line whatsoever: instead, electrons of definite energy (in an eigenstate) are represented spatially for hydrogen like this:

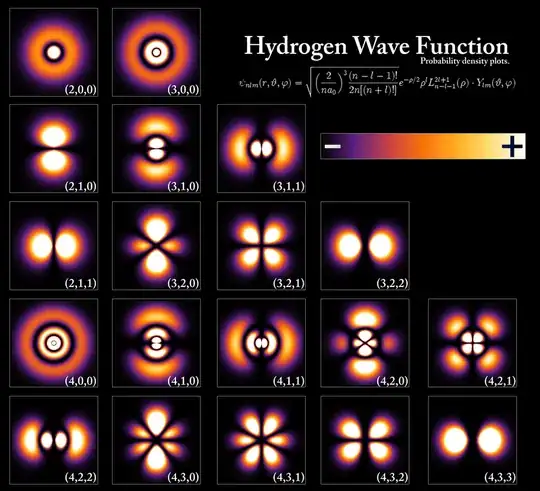
The following description glosses over quite a few details but should give you the basic idea: If you imagine some continuous wave-like transformation (think waves in a pond) from one of these 'states' to another, that represents an electron transition from absorbing or emitting a photon. There is so much more going on here, but at the conceptual level, I think this is the biggest leap you have to make: electrons are better described as waves than particles.

Answer 2

Does it go from one state to another via straight line or it makes smaller and smaller orbits till it reaches the next orbit

The electron is an elementary particle and as such, at the level of atoms, it can only be mathematically modeled by a quantum mechanical probability distribution. These spatial probability distributions for the electron of the hydrogen atom are shown in the answer by anon0909. They are called orbitals, not orbits. They will be different distributions for a hydrogen atom with an electron at an excited state, i.e. a "hole" in a lower energy level to which the electron can transition by emitting a photon.This probability distribution will have a very large spatial peak at the "hole" space, i.e. there is a very high probability for the electron to appear at the space locus of the hole with a photon departing.

In the sense of probabilities, in principle the electron has a probability to exist anywhere in space. Electrons in bound states have zero probability ( infinitesimally small) to be outside the probability loci shown. For unstable configurations one has to calculate the probability distribution for the problem.

An electron manifests as a particle in macroscopic measurements, with a probability distribution , as in the double slit single electron on the screen, as a dot while the probability distribution of the accumulation shows wave properties. One can only model mathematically the electron around an atom. Its orbital can be inferred by proxy, from the energy of the photon emitted, not from the electron itself. The model that fits the data is a quantum mechanical model that can only give the probability of the electron to be at (x,y,z, t).

If you want to imagine the probability orbital during the deexcitation of the electron, you could think of it as a probability locus which is variable in time ( the width of the spectral line) . Within delta(t) it will be a probability cloud for the location of the electron (x,y,z,t) joining the higher energy state orbital probability locus to the lower energy state one.