I created a bounce simulation using exactly the formula from Wikipedia. The behavior I observe is not what I would expect in two cases:
When two balls hit off-centre, they act the same as if the impact was face-on.
Click for animation
When a small ball hits big ball (with gravity), it bounces back and forth in arc, not around the big ball: animation.
Is this behavior consistent with the inelastic equation formula?
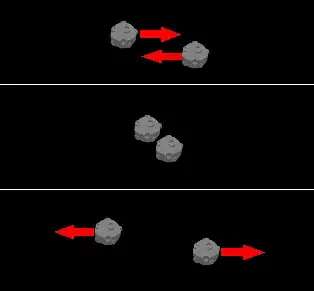
For a 2D planar simulation with zero friction do the following
The contact normal (force) direction is $$ n = \begin{pmatrix} \cos \psi \\ \sin\psi \\ x_A \sin\psi - y_A \cos \psi \end{pmatrix}$$ Note that the velocity of body 1 on the contact point, along the contact normal is found by $n \cdot v_1 = n^\top v_1 = (\dot{x}_1+\dot{\theta}_1 (y_1-y_A))\cos\psi + (\dot{y}_1-\dot{\theta}_1 (x_1-x_A))\sin\psi$
The inverse inertia matrix for each body is
$$ \begin{aligned}I_{1}^{-1} & =\begin{vmatrix}\frac{1}{m_{1}}+\frac{y_{1}^{2}}{Iz_{1}} & -\frac{x_{1}y_{1}}{Iz_{1}} & \frac{y_{1}}{Iz_{1}}\\ -\frac{x_{1}y_{1}}{Iz_{1}} & \frac{1}{m_{1}}+\frac{x_{1}^{2}}{Iz_{1}} & -\frac{x_{1}}{Iz_{1}}\\ \frac{y_{1}}{Iz_{1}} & -\frac{x_{1}}{Iz_{1}} & \frac{1}{Iz_{1}} \end{vmatrix} & I_{2}^{-1} & =\begin{vmatrix}\frac{1}{m_{2}}+\frac{y_{2}^{2}}{Iz_{2}} & -\frac{x_{2}y_{2}}{Iz_{2}} & \frac{y_{2}}{Iz_{2}}\\ -\frac{x_{2}y_{2}}{Iz_{2}} & \frac{1}{m_{2}}+\frac{x_{2}^{2}}{Iz_{2}} & -\frac{x_{2}}{Iz_{2}}\\ \frac{y_{2}}{Iz_{2}} & -\frac{x_{2}}{Iz_{2}} & \frac{1}{Iz_{2}} \end{vmatrix}\end{aligned} $$
The impact velocity (scalar) is $$v_{imp} = -n^\top (v_2-v_1)$$
The inverse effective mass (scalar) along the contact of each body is $$\begin{aligned}\mu_{1}^{-1} & =n^{\top}I_{1}^{-1}n & \mu_{2}^{-1} & =n^{\top}I_{2}^{-1}n\end{aligned} $$
The impulse acting on body 2 is $$\boxed{ J = \frac{(1+\epsilon)\;v_{imp}}{\mu_{1}^{-1}+\mu_{2}^{-1}} } $$
The impact $J$ acting along $n$ changes the motion of each body by $$ \begin{aligned}\Delta v_{1} & =-I_1^{-1} n\,J & \Delta v_{2} & =I_2^{-1} n\,J\end{aligned} $$
The changes in motion are transferred back to the center of mass (change in) velocities $\Delta \dot{x}_1$, $\Delta \dot{y}_1$ and change in spin $\Delta \dot{\theta}_1$ by solving the following definition
$$\begin{aligned} \Delta v_1 &= \begin{pmatrix} \Delta \dot{x}_1 + \Delta \dot{\theta}_1 y_1 \\ \Delta \dot{y}_1 - \Delta \dot{\theta}_1 x_1 \\ \Delta \dot{\theta}_1 \end{pmatrix} & \Delta v_2 &= \begin{pmatrix} \Delta \dot{x}_2 + \Delta \dot{\theta}_2 y_2 \\ \Delta \dot{y}_2 - \Delta \dot{\theta}_2 x_2 \\ \Delta \dot{\theta}_2 \end{pmatrix} \end{aligned}$$
$$\begin{aligned}\dot{x}_{1} & \leftarrow\dot{x}_{1}+\Delta\dot{x_{1}} & \dot{x}_{2} & \leftarrow\dot{x}_{2}+\Delta\dot{x_{2}}\\ \dot{y}_{1} & \leftarrow\dot{y}_{1}+\Delta\dot{y_{1}} & \dot{y}_{2} & \leftarrow\dot{y}_{2}+\Delta\dot{y_{2}}\\ \dot{\theta}_{1} & \leftarrow\dot{\theta}_{1}+\Delta\dot{\theta_{1}} & \dot{\theta}_{2} & \leftarrow\dot{\theta}_{2}+\Delta\dot{\theta_{2}} \end{aligned} $$
No. Momentum is still conserved. In particular, the component of momentum parallel to the ground is conserved. So if the ball is going to the right before hitting the ground, it will continue going to the right after.
The formula you refer to is for one-dimensional collisions. That applies only if the elements are arranged so that there actually is motion in only one dimension. Your two balls would deflect off each other because they hit off center. They would each start moving partially in the vertical direction -- with equal components of momentum in the vertical direction.
