How does the electrons' magnetic dipole moment get influenced when electrons are moving through a magnetic field?

Question

How does the electrons' magnetic dipole moment get influenced when electrons are moving through a magnetic field? How does the electrons' intrinsic spin influence the direction of the electrons' movement during the alignment of the dipole moment to the external magnetic field?

Answer 1

How the electron's magnetic dipole moment gets influenced when electrons are moving through a magnetic field?

In a classical context, the dipole moment of a fundamental particle is fixed: it doesn't change when in an electromagnetic field. If Nature were classical, the dipole moment of electrons would be $\boldsymbol\mu=2\mu_B\boldsymbol S$, where $\mu_B$ is the Bohr magneton ($\mu_B=5.8\ 10^{-5}\ \mathrm{eV/T}$) and $\boldsymbol S$ is the intrinsic spin of the electron (whatever that means: in a classical context, spin is not well defined. Spin is an intrinsically quantum phenomenon). If you place this electron in a magnetic field, it will feel a torque, but the value of $\boldsymbol \mu$ won't change.

In QM, there is always a magnetic field (in a certain sense). You cannot isolate fundamental particles from interactions with the electromagnetic field. This in turns changes the value of the dipole moments in a well-defined way (through radiative corrections). These changes are usually very small: for example, in the case of electrons, the formula above changes into $\boldsymbol \mu=2.0023\mu_B\boldsymbol S$. Photons are responsible for this small change.

How the electron's intrinsic spin agitate on the direction of the electrons movement during the alignment of the dipole moment to the external magnetic field?

Let $\boldsymbol \mu$ be the dipole moment of a particle, and $\boldsymbol S$ its spin. In general we can write $$ \boldsymbol\mu=g\mu_B\boldsymbol S $$ where $\mu_B$ is the Bohr magneton, and $g$ is the $g$-factor. According to Newton's Second Law, $\dot{\boldsymbol S}=\boldsymbol\mu\times \boldsymbol B$, from which we find $$ \dot{\boldsymbol S}=g\mu_B \boldsymbol S\times\boldsymbol B $$ whose solution is a precession of $\boldsymbol S$ around $\boldsymbol B$: $$ \begin{aligned} \boldsymbol S_\parallel(t)&=\boldsymbol S_\parallel(0)\\ \boldsymbol S_\perp(t)&=\boldsymbol S_\perp(0)\ \mathrm e^{-i\omega_s t}\\ \end{aligned} $$ where $\omega_s=g\mu_BB$

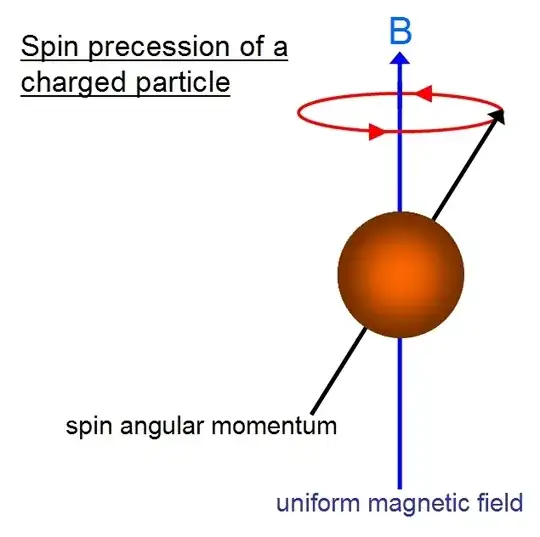(borrowed from http://cronodon.com/Atomic/quantum_angular_momentum.html)

For completeness, we should point out that if the magnetic field is inhomogeneous ($\boldsymbol B=\boldsymbol B(\boldsymbol r)$) then the dipole will also feel a transaltional force. The easiest way to see this is that the potential energy of a dipole is $W=-\boldsymbol \mu\cdot\boldsymbol B$, so that $$ \boldsymbol F=-\nabla W=\nabla(\boldsymbol\mu\cdot\boldsymbol B)\neq 0 $$

Only in the case of constant magnetic field $\nabla\boldsymbol B=0$, and we only get rotational motion. If $\boldsymbol B$ is inhomogeneous, there is also a translational force.