3

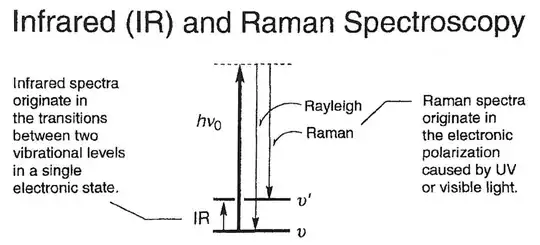
Raman spectroscopy essentially records photoluminescence: enter image description here(source)

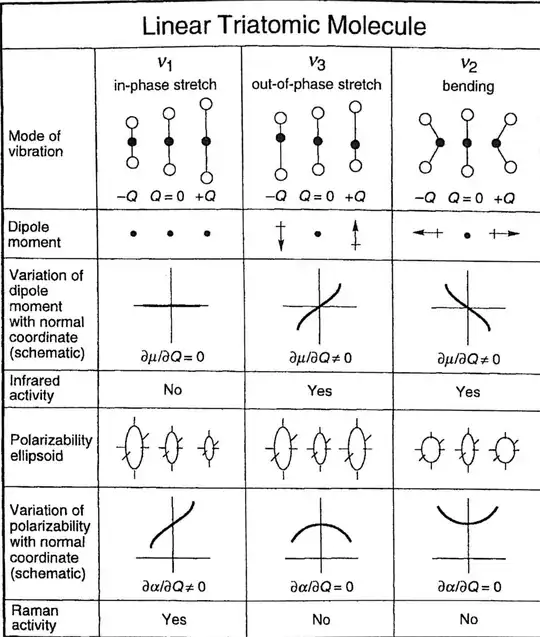
and a molecule is considered to be Raman active when there is a change of polarizability $\alpha$ (where $\mathbf{P}=\alpha \mathbf{E}$) during vibration, $\left(\frac{\partial \alpha}{\partial Q_k}\right)_0 \neq 0$:

enter image description here(source)

On the other hand, in general terms, intensity of emission is proportional to the transition moment, $$\mathrm{TM} = \langle \Psi_i | \mu | \Psi_f \rangle$$ where $\Psi_i, \Psi_j$ are the initial and final molecular wavefunctions, and $\mu = q_e \sum \vec r_i$ is the dipole moment. This expression doesn't seem to be related to polarizability.

Then why would electronic transitions ($\Psi_i\to\Psi_f$, i.e. photoluminescence yield) depend on polarizability? In other words, why does Raman activity depend on polarizability?

Sparkler
  • 3,324

1 Answers1

1

The laser is providing a periodic electric field and we are anticipating that energy is going to be either lost or gained due to the absorbtion or emission of a phonon. The absorbtion and emission of a phonon is detectable by observing sidebands in the scattered light.

As you've mentioned:

$$\textbf{P} = \alpha \textbf{E}$$

where:

$$\textbf{E} = E_0 cos(\omega_{Laser} t)$$ $$\alpha = \alpha_0 + \frac{d \alpha}{d Q} cos(\omega_{Phonon} t) $$

Therefore, when \frac{d \alpha}{d Q} is non-zero:

$$\textbf{P} = \alpha \textbf{E}$$ $$= [\alpha_0 + \frac{d \alpha}{d Q} cos(\omega_{Phonon} t)] E_0 cos(\omega_{Laser} t)$$ $$= \frac{d \alpha}{d Q} ( cos(\omega_{L} t +\omega_{P} t) + cos(\omega_{L} t -\omega_{P} t)) $$

(ignoring some factors of 2 that will affect the amplitude). Here we see that the scattered light features sidebands that are at frequencies $\omega = \omega_L \pm \omega_P$.

In the case where $\frac{d \alpha}{d Q} = 0$:

$$\textbf{P} = \alpha \textbf{E}$$ $$= \alpha_0 E_0 cos(\omega_{Laser} t)$$

and the scattered light does not feature sidebands.

JakeA
  • 112