I shall try here to prove the statement posted in your question, but I have to admit that this is an effort with one particular danger; since I'm not a mathematician I can only rely on others with more knowledge from me, so that, any mistakes in the formality of my proof or any inconsistencies on the mathematics involved may be found and corrected. So, having said that:
We can define the δ Dirac function as follows:
$$δ(x)= \lim_{n\to \infty} D_n (x) .$$
Some examples or D functions are ${{\sin(nx)} \over {πx}} $ or $ \sqrt{{{π} \over {n}}e^{-nx^2}} .$
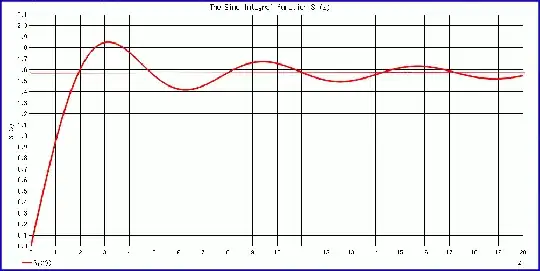
We want to prove the same for: $$D_n (x)= {{\sin(ax)} \over {πax^2}}=δ(x). $$
So from the definition of Dirac function: $\int_{- \infty}^{\infty} f(x) δ(x) = f(0), $ we shall deal with this relationship:
$$ I= \lim_{a\to \infty}{ \int_{- \infty}^{\infty} (f(x) – f(0)){{1} \over {π}} {{\sin^2 (ax) } \over {ax^2}} dx } =0 ,$$ where we brought $f(0)$ in the integral by noticing:
$$\int_{- \infty}^{\infty}{{1} \over {π}} { {\sin^2 (ax)} \over {ax^2}} =1 , $$ for positive a.
For this problem to have meaning, $f$ must be a continuous function at 0. So, it must hold:
$$|x|<δ \rightarrow |f(x) – f(0)| < ε $$, were δ,ε some arbitrary numbers for now. Now we make the change $ax=t $. Taking the above integral, we have:
$$A= \int_{- \infty}^{\infty} (f(t/a) – f(0)){{1} \over {π}} {{\sin^2 (t) } \over {t^2}} dt $$
so that
$$ A \leqslant { {1} \over {π} } \left[ \int_{- \infty}^{\infty} |f(t/a) - f(0) |^2 dt \right]^{1/2} ~~~\left[ \int_{- \infty}^{\infty} \left|{{\sin^2 (t)} \over {t^2}} \right|^2 dt \right]^{1/2} .$$
The inequality came from using the Cauchy-Schwarz inequality. We set $ A_1$ the first integral term and $A_2 $ the second. So:
$$A_1 = \sqrt { \int_{- \infty}^{\infty} |f(t/a) - f(0) |^2 dt } \leqslant ε \sqrt{δa}, $$ where this result came from the continuity considerations of $f$. Also,
$$ [ \int_{- \infty}^{\infty} \left|{{\sin^2 (t)} \over {t^2}} \right|^2 dt \leqslant \prod \left[2 \int_0 ^{ \infty} {{\sin t} \over {t}} dt \right]^{1/2} = 4π, $$ where we again used the Cauchy-Schwarz inequality if I have understood correctly (see also http://arxiv.org/abs/1405.1265).
So, we have, in the end:
$$A=A_1 A_2 \rightarrow A \leqslant ε \sqrt{δa} .$$
For certain, fixed values of δ,α we may choose ε so that the term is close to zero, thus having:
$$I= \lim_{a\to \infty} A =0 .$$
I am sure there might exist mistakes but if anyone with more knowledge is interested he/she 's welcome to correct them.
Hope this helps.