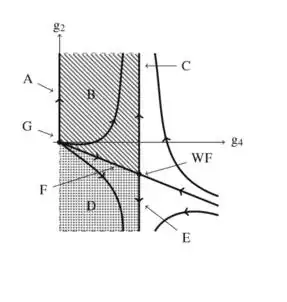
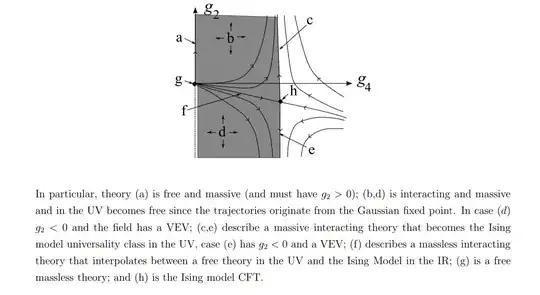
I'm having trouble making sense of this phase diagram. The model is a $V(\phi)=g_2 \phi^2+g_4\phi^4$ scalar field theory. Here's what I think I understand: the capital letters represent different phases (the B and D phases have the hatched areas associated with them, while all other phases occupy only lines or points in the phase diagram rather than entire areas). G is the Gaussian fixed point and WF the Wilson-Fisher fixed point. Define $\ell=\log\left (\frac{\Lambda_0}{\Lambda}\right)$, where $\Lambda_0$ is the original cutoff of the theory and $\Lambda$ is the scale that you're viewing it (you've integrated out all the modes between $\Lambda_0$ and $\Lambda$, $\Lambda<\Lambda_0$). The arrows in the trajectories on the phase diagram point towards increasing $\ell$.
The first question is did I get the above description correct?
Second, to take the continuum limit $\Lambda_0 \rightarrow \infty$ but keep the same scale you're viewing the system $\Lambda$, $\ell$ must then go to $\infty$. That suggests to take the continuum limit from any point on one of the trajectories, you just follow the arrows. But that seems to suggest that only systems on the line going through the points G and WF have continuum limits, since everywhere else the arrows are leading to infinite mass $g_2$ which seems to be nonsense. However, I have my doubts about saying that only the line G-WF has a continuum limit, because the author (Hollowood) makes the statement that the region to the right of the line joining C and E has no continuum limit, implying that everything to the left of that line does have a continuum limit.
Third, consider changing the scale that you look at $\Lambda$. Increasing this scale (probing the UV) while keeping $\Lambda_0$ fixed amounts to decreasing $\ell$, so you would follow the arrows backwards to see what happens in the ultraviolet. In regions B and D the UV behavior is sensible (finite values of mass and coupling - zero in fact), but the IR behavior (in the direction of the arrows) is nonsensical as parameters are flying off to infinite. If you have one theory that is supposed to describe everything at all scales, then do all trajectories must begin and end at finite fixed points?
Lastly, it seems increasing $\Lambda$ and keeping $\Lambda_0$ fixed, or keeping $\Lambda$ fixed and decreasing $\Lambda_0$, both decrease $\ell$. Does this mean keeping the grid the same but viewing it at a increased resolution is indistinguishable from putting the system on a coarser grid but keeping the resolution the same?