Single Photon Single Slit Interferometry

Question

If just a single photon hit a single slit interferometer, what would happen? Would you just see a dot on the screen, or would there be a diffraction pattern? Furthermore, if you had a double slit interferometer but also had which-path information would there still be a diffraction pattern even though there is no interference?

Answer 1

When a single photon hits a screen, it can only create a dot at the point where it is detected. Thus, the short answer to your question is "yes, you would just see a dot".

However, it is clear from the various comments on this page that you are looking for deeper insight, and that the concept of a "photon interfering with itself" is confusing and potentially misleading.

The behavior of a photon is at times best described by calling it a particle; at other times, its behavior looks like that of a wave. The dual slit experiment attempts to demonstrate this duality.

As the photon "wave" passes through the slits, it actually passes through both slits, like a wave would. The result of this is that the wave, after the slit, gets certain peaks and troughs - there are certain "preferred" directions for the wave, while the amplitude in other directions is diminished. But when the photon "wave" interacts with the screen, the photon can only be observed at a single place. In quantum mechanics, they say "the wave function collapses".

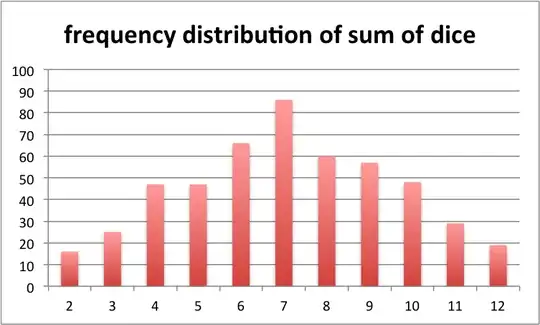
Here is the fun bit: the single photon could have appeared just about anywhere on the screen - but it only appeared in one place. This is where probability comes into play - similar to the example given by Anna V, if you roll a pair of dice, the sum could be any number from 2 to 12. But for a given roll, you only see a specific sum - for example, 5. If I asked you to guess the number, your best guess would be "7", because for a pair of dice, the probability of the sum being 7 is higher than any other value (1-6, 2-5, 3-4, 4-3, 5-2, 6-1 are the 6 rolls that could get you 7. Any other number has fewer possible combinations). Now when you roll the dice just once, you get a particular sum (like the photon hitting the screen at just one place); if you roll the dice many times, and plot the number of occurrences of each sum, you get a triangular distribution (example after 500 random rolls):

And so it is with photons going through slits. The act of going through the slit changes their wavefunction in such a way that the probability of them landing at a particular point on the screen is no longer uniform; but when they do land, they land in a particular location; it is only by observing a large ensemble of photons that you start to see this pattern emerge - there will be more dots in some regions than in others.

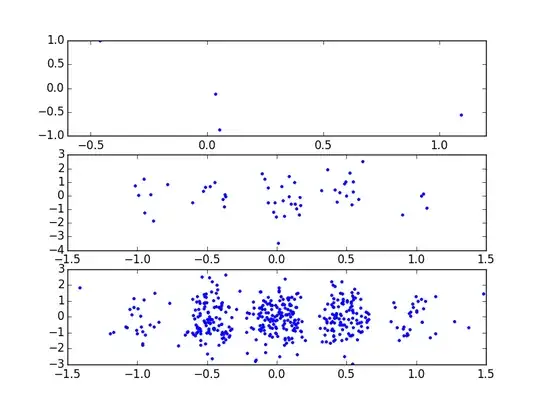
I wrote a little simulation to demonstrate this - each plot has ten times more dots than the one before. In the first plot you have just a few dots, with no pattern; in the next row, a pattern starts to emerge; in the bottom row, the interference pattern is clear. But in each case, an individual photon lands in just one place.

If you are interested in reproducing a graph like this, here is the (rather crummy) code I used to generate it. Don't rely on this as either "good code" or "good physics" - it was purely designed to illustrate the concepts above.

import matplotlib.pyplot as plt
import numpy as np
import math

def pattern(w, d, l, a):
  if a==0:
      sinc = 1.0
  else:
      sinc = math.sin(a*w/l)/(a*w/l)
  p=math.cos(a*d/(math.pi*l))*sinc
  return p*p

w = 1e-6
d = 1e-5
l = 5e-7

plt.figure()
for ni,n in enumerate([20, 200, 2000]):
    dots=[]
    X=np.random.uniform(low=-1.5,high=1.5,size=n)
    Y = np.random.uniform(size=n)
    for x in X:
        if np.random.uniform() < pattern(w,d,l,x):
            dots.append(x)
    plt.subplot(3,1,ni+1)
    plt.plot(dots, np.random.normal(size=len(dots)),'.')
plt.show()

Answer 2

There would never be a pattern with only one photon. No matter how many slits or even if you have information about the photons path. It would probably take thousands of photon impacts to form a recognizable pattern. Also remember not every photon will make it to the detection screen.

Answer 3

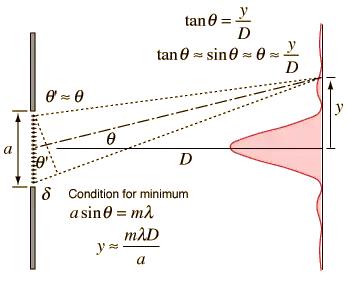
Here is the Fraunhofer singles slit interference

The diffraction pattern at the right is taken with a helium-neon laser and a narrow single slit.

This is a light beam composed out of zillions of photons. The fact that the photon is a quantum mechanical entity implies that this difraction pattern is the probability distribution for an individual photon going through the slit.

Each individual photon gives one spot on the screen ( the image on the right). The accumulation shows the interaction of the photon as it scatters in the field of the electrons that define the edges of the slit. It is the complex conjugate square of the photon's wave function. It gives the probability of finding the photon at a particular y on this plot.

Even for a classical set up, a slit and balls thrown at it, if the ball was of the order of magnitude of the slit width the errors would introduce an uncertainty and the balls would scatter at the edges at an angle , so not all balls thrown one at a time would fall on the same y. The probability would be a gaussian due to the errors, but no interference. In quantum mechanics there are no edges, there are fields and particles interacting with the fields and the position y given by sinusoidal solutions of the applicable differential equations. In the case of the photon it is Maxwell's equation turned into operator format. So the probability instead of being a gausian shows the maxima and minima of a wave pattern.

The double slit is covered by other answers. This experiment shows that again , the interference pattern depends on the boundary conditions which change with which way detection.

Answer 4

Please read at first Annas answer.

Anna, you clearly pointed out that "The accumulation shows the interaction of the photon as it scatters in the field of the electrons that define the edges of the slit". Fringes we get behind single edges too. The same phenomenon takes place on a single edge, so it's not necessary to talk about slits at all.

Now it has to be proofed whether the photons wave function alone is responsible for the intensity distribution or the electric field of the involved surface electrons of the edge(s) are responsible together with the electric field component of the photon. I articulated this point here Can the intensity distribution behind edges and slits be explaint by the interaction with the surface electrons of the edges? and in more details in my papers here and - if you have enought time to read her.

Answer 5

If you are using only a single photon, you'd of course see only a dot in the screen in both the cases.

But if you use enough photons (but one at a time) then you will see that each of them are hitting the screen in different positions and the distribution of dots will be like the diffraction pattern in case of single-slit interferometer.

In case of double-slit if you have which path info then with the above technique of one-photon-at-a-time you'd get two normal single slit distributions overlapped.