The formula for potential energy regarding point charges is $E=kQq/r$. If $r=0$, then will the energy be approaching infinity?
But what about an electron in a parallel-plates situation where it is right beside the negative plate? There is a defined voltage between the two plates, and the potential energy of the electron is $E=q\Delta V$. The energy clearly isn’t infinite. So why is it infinite in the point-charges situation? Or is it not?
This answer addresses the infinity question in the OP.
You are using Coulomb's law, a classical physics law derived by observations, and even in classical physics the $1/r$ behavior cannot be carried to the limit of 0 radius. In particular your electron next to a negative plate has a complicated solution similar to the discussion in another question here . One has to use Maxwell's equations to solve for the case rigorously.It is only for two point charged particles that a mathematical infinity is implied, BUT point particles belong to the microcosm, and nature at small distances is quantum mechanical.
The electron is an elementary point particle, and quantum mechanics enters for elementary particles. In the quantum mechanical equations the 1/r potential controls the solutions, but the behavior of the particle is probabilistic.
When scattering an electron on an electron, for the radius of separation to be zero, infinite momentum would be needed due to the Heisenberg Uncertainty Principle ( HUP).
$$\sigma_x\sigma_p\geq \frac{\hbar}{2}$$
Thus an electron can "stay" as close to another electron as the momentum ( energy) supplied to keep it there.
In the case of the attraction of an electron to a proton the solutions of the quantum mechanical equations give bound states.
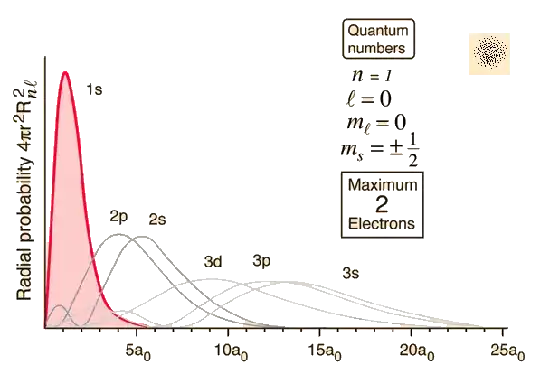
The $1/r$ potential is in the Schroedinger equation for the solutions of the system in the link above, and the solutions have no infinities. $a_0$ is the bohr radius = 0.0529nm
Bearing in mind that we're talking about ideal systems that don't really exist:
When you have point charges all the charge is localised at a point. So when you reach that point all the charge is a zero distance away from you. Hence the infinite force.
In a parallel plate capacitor the charge is spread out over the plate with some area $A$. If we take some part of this area $\delta A$ then the charge in that area is:
$$ Q = \sigma\delta A $$
where $\sigma$ is the surface charge density.
Suppose you're a point charge and you've just reached the plate. The area that is within some distance $dr$ from you is:
$$ \delta A = \pi dr^2 $$
So the charge within a distance $dr$ of you is:
$$ Q = \sigma\pi dr^2 $$
To get the charge that is a zero distance from you we have to let $dr \rightarrow 0$ so we get:
$$ Q = \sigma\pi 0^2 = 0 $$
And there's your answer. The amount of charge at zero distance from you is zero so the force on you from that charge is zero. There is still a force on you of course, but that force is the sum of all the forces from the charge that isn't at zero distance from you, and that force remains finite.
Notice, for $r=0$, how can you say that it is the system of two point charges or how can you apply the formula $E=\Large \frac{kQq}{r}$?
The formula of potential energy $E=\Large \frac{kQq}{r}$ is defined for the system of two point charges which are separated by a finite distance $r>0$ so if the point charges are brought very closer i.e. $r\to 0$ then the potential energy $E\to \infty\ $ (but $E\ne \infty$) i.e. the energy is too large but it has some large finite value.
but if one considers $r=0\implies E=\frac{kQq}{r}=\infty$ then it means that the point charges have coincided together (into a single point charge) & so the system of two point charges is no more in existence i.e. such system of charges is undefined. Hence in case of $r=0$, the energy $E$ is infinity i.e. $E$ is undefined.
