Quantum Erasure Spookiness

Question

First off - I am not an expert. I am intrigued by quantum physics and have a layman's understanding at best. I've looked at other questions, but either the answers are not answering my question, or I've failed to understand the answer (entirely possible). If the latter, then if I could trouble you for a simple explanation, I would appreciate it.

I was reading this article. In the "Quantum Eraser" section at the bottom, there is the following text:

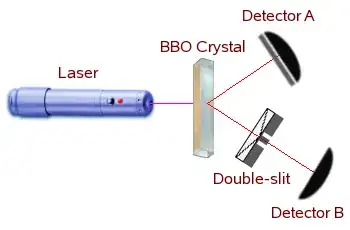
Figure 6.5 shows a Bell-state quantum eraser, named after John Bell. It illustrates the application of the following steps:

1. a laser fires photons into a Beta Barium Borate (BBO) crystal;
2. the crystal entangles some of the photons; and then
3. entangled photons travel to two different detectors: A and B.

Placed between the crystal and detector B is a double-slit, like in the previous experiments. Immediately in front of detector A is a polarizing filter that can be rotated. Figure 4.5 showed an experiment using sunglasses to see the effects of rotating a polarizer. Those same effects apply here.

The Bell-state quantum eraser has one more feature: each slit is covered by a substance that filters the polarization of a photon. Consequently, the left-hand slit will receive photons with a counter-clockwise polarization, and the right-hand slit will pass photons with a clockwise polarization.

Note: Polarization does not affect interference patterns.

Initially, neither detector shows an interference pattern. Since we control the polarization of photons passing through the slits and we know the polarization accepted by each slit, we can deduce which way the photons travelled (counter-clockwise through the left; clockwise through the right). Thus no interference patterns are detected.

However, if we rotate the polarizing filter in front of detector A so that the polarizations of the photons that hit the detector are the same (that is, we can no longer distinguish between clockwise and counter-clockwise polarizations), then the interference pattern appears at both detectors!

How do the photons arriving at detector B know that the polarizations have been "erased" at detector A?

I find this result fascinating, and disturbing. By rotating the filter at A, I can change the interference pattern at B. In fact, if I was in charge of the filter at A and a friend was watching detector B, they could tell when I rotated the filter right? If so, then isn't this communication?

If A and B are spatially separated by many light years, wouldn't this even be FTL communication?

Is there something wrong with the article I linked? Perhaps I am misunderstanding it, but it seems pretty clear to me.

Answer 1

Let's denote the photon going through the left slit by $\vert L\rangle_B$, and the one going through the right slit by $\vert R\rangle_B$. The photon pair is prepared in the entangled state $$ \vert L\rangle_A\vert L \rangle_B + \vert R \rangle_A\vert R\rangle_B\ . $$

If we now measure the $A$ photon in the $\vert L\rangle$, $\vert R\rangle$ basis, we obtain the which-way information and no interference pattern is observed.

Let us now consider the case where we erase the which-way information, i.e., measure in the basis $\vert L\rangle \pm \vert R\rangle$. Let us first consider the $+$ outcome. Then, the $B$ photon is in the state $\vert L\rangle + \vert R\rangle$ and the two paths will interfere. This is, the photon will be observed at a position $x$ with a probability $p_+(x)$ which describes an interference pattern.

Let us now consider the $-$ outcome. Then, the photons are in the state $\vert L\rangle-\vert R\rangle$, i.e., as compared to the $+$ outcome, the photon going through the right slit will experience a phase shift of $\pi$. This phase shift will lead to a distribution $p_-(x)$ of photons on the screen which is shifted by half a spacing with respect to $p_+(x)$ (i.e., dark and light are interchanged).

Now in order to observe the interference pattern, $B$ will have to detect many (or at least more than one) photon. However, for each photon, the outcomes $+$ and $-$ will be distributed randomly: the overall pattern observed by $B$ will thus be distributed according to $q(x)=(p_+(x)+p_-(x))/2$. Since the two distributions are shifted by half a spacing, the distribution $q(x)$ observed by $B$ will show no interference pattern, just as if $A$ had measured in the which-way basis.

(Note that if $B$ records the position for each photon and $A$ and $B$ later compare their data, they will indeed find that the photons with a $+$ outcome and the photons with a $-$ outcome individually did form an interference pattern; however, since the outcomes were random $B$ had no way of identifying these patterns prior to learning the outcomes.)

Answer 2

I find this result fascinating, and disturbing. By rotating the filter at A, I can change the interference pattern at B.

It's not like that. Interference pattern at B is observed only by ignoring all of the photons whose entangled twins never reached A (only coincident photons are counted).

It's easy to see that by rotating polariser in front of A you change which photons never reach A (and which thus you choose to ignore at B).

By rotating polariser at A you just stop considering the photons that are giving interference pattern at B and start considering those that don't.

So not FTL possible because guy at A must still tell B by normal channels which photos to ignore to either see or not see interference pattern.