Confusion about the concept of cosmological horizon

Question

This question was inspired by this one

By definition we cannot see any event happening beyond the cosmological horizon. Let us assume that the expansion rate of the universe is such that the radius of the cosmological horizon is constant and centered at the observer (perhaps this assumption is inconsistent?). Now suppose I move 100 light years in one direction to meet another observer. This second observer has a different cosmological horizon, shifted in the direction the I moved. Hence I will be able to see events that I could not see before my trip, because they were outside my cosmological horizon. Then I travel back and show my friends a video of the event. How is that possible if the event was always beyond their cosmological horizon? (My trip should not be able to overcome that limitation, correct?)

Answer 1

I will assume that you mean by cosmological horizon the cosmological event horizon. Now, there are two possibilities:

1. You travel to a region that is (still) located inside the event horizon of the Earth. Then, by definition, the light that you observe at that location will also eventually reach the Earth (if it hasn't already). In fact, that light will have reached the Earth before you have travelled back, so you'll have nothing new to tell you fellow Earthlings.

2. You travel to a region that is located outside the event horizon of the Earth. Then, again by definition, you are able to see light that will never reach the Earth. However, nothing can reach the Earth: you can no longer travel back either, nor can you send any signals to Earth. Once you are outside the Earth's event horizon, you are cut off from Earth forever.

In other words, the region that you travelled to might have its own event horizon, but that doesn't matter. What matters is whether or not you are still inside the event horizon of the Earth. If you are, then the Earth will receive the same information as you, and before you can make it back. If you aren't, then you can no longer communicate with the Earth, let alone travel back.

A final word of caution. A different region of space doesn't necessarily have a different event horizon. The FLRW metric is an idealization, and only valid on large scales. A region that is e.g. 100 light years away is gravitationally bound to us, and in the Standard $\Lambda$CDM model it will remain gravitationally bound. Since all observers in a bound structure can send signals to each other, they all share the same cosmological event horizon.

Answer 2

The cosmological horizon is constantly expanding with time. When you were relocating, the expansion of the cosmological horizon was faster in the direction you were traveling and slower behind you. When you got to the other observer and stopped, you both had the same cosmological horizon. That cosmological horizon was larger than your original cosmological horizon and completely encloses your original cosmological horizon because you had to travel slower than light.

When you were returning to your original location, the expansion of the cosmological horizon was faster in the return direction and slower behind you. So, once you stopped at your original location, your original cosmological horizon and your now larger current cosmological horizon have the same center. As before your new cosmological horizon completely encloses the cosmological horizon you had while you were at the other observers location.

The other observers new cosmological horizon has a different center, but he can currently see part the universe that is currently outside your cosmological horizon (in the direction away from you), and you can currently see part the universe that is currently outside his cosmological horizon (in the direction away from him).

Answer 3

Let me try and rephrase your question to make it simpler to answer. Suppose you are a comoving observer in a de Sitter universe, then you are at the centre of a spherical event horizon with some constant radius $R$:

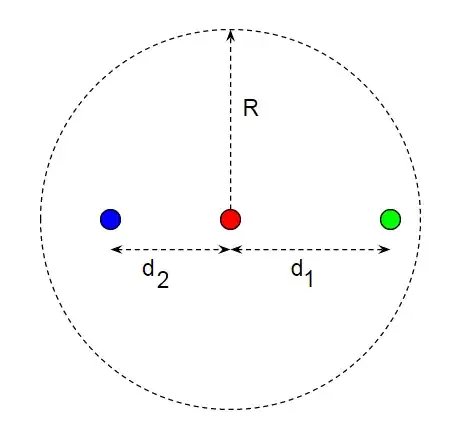
You can receive a signal from the green dot because it's inside your horizon, and you can send a signal to an observer at the blue dot because it's inside your horizon. The sum of the distances $d_1 + d_2$ can have any value less than $2R$, but doesn't that mean an observer at the blue dot can receive signals from the green dot at a distance greater than $R$ i.e. from outside their horizon?

To understand what is going on you need to consider the motion of the observer at the blue dot. There are three main cases:

1. the blue observer is a comoving observer, in which case they are moving away from you with velocity $Hd_2$, and is being accelerated away from you by the expansion.

2. the blue observer is momentarily stationary with respect to you, but is being accelerated away by the expansion.

3. the blue observer remains stationary relative to you using some form or rocket motor.

Case 1 is the easy case since in the time the signal takes to reach you from the green dot the blue observer will have accelerated away. If the sum of $d_1 + d_2 > R$ then by the time you receive the green signal the blue observer will be on a trajectory that outpaces the signal you send so they'll never receive it.

Case 3 is harder because the position of the horizon will be different for a non-comoving observe. The acceleration will contract the horizon distance opposite to the blue observer and extend it in your direction. This does indeed allow the blue observer to receive signals from a distance greater than $R$ in the direction of the acceleration. The flipside is that the horizon moves inwards in the opposite direction.

Case 2 I confess I'm not sure about. I would have to do some calculations to convince myself I understood what was going on, however it seems plausible that a non-zero peculiar velocity would affect the horizon position.

All this is qualitative, and to make it concrete you'd need to calculate the geodesics of the light and the geodesics of the blue observer. I'll think on this, but I suspect this is a messy calculation to do.