Infalling light signals seen by a free falling observer

Question

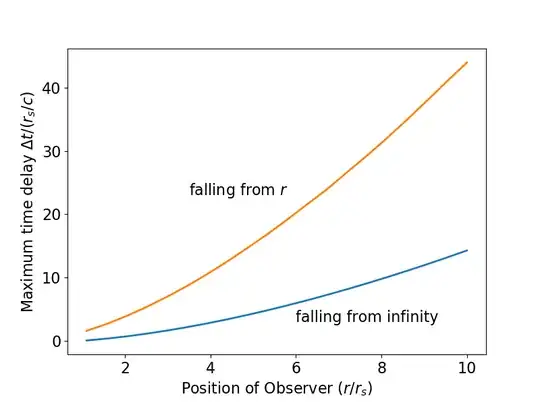
In this question/answer Does someone falling into a black hole see the end of the universe?, it is stated that an observer free falling toward/into a black hole will not see the end of the Universe because the worldline of that observer in Kruskal coordinates crosses the horizon and terminates at the event horizon without seeing all infalling light signals, which would be required in order for that observer to see the end of the Universe.

But outside the horizon, where Schwarzschild coordinates are applicable, it takes an infinite amount of coordinate time (though not proper time) to reach the horizon and therefore, in those coordinates outside the horizon, wouldn't all infalling light signals intersect the freefalling observer's path before or at the horizon (since the amount of Schwarzschild coordinate time for the light signal to reach the horizon must also be infinite)?

Given that a timelike free falling observer must follow a path defined such that $\left|\frac{dr}{dt}\right|$ of that path is always less than the $\left|\frac{dr}{dt}\right|$ of the worldline of any given light signal at a given $r$, it seems to me that all light signals should intersect the free falling observer's worldline before reaching the horizon (since an infinite amount of coordinate time passes before either reaches the horizon).

Why is incorrect to interpret the consequence of the Schwarzschild coordinates (which are applicable for $r>r_s$) in this way?

Note added in edit by RJ: For a free-falling observer $$\left(\frac{dr}{dt}\right)_{\rm obs} = -\left(1 - \frac{r_s}{r}\right)\left(\frac{r_s}{r}\right)^{1/2},$$ (in $c=1$ units), whereas the null geodesic for light has $$ \left(\frac{dr}{dt}\right)_{\rm light} = -\left(1 - \frac{r_s}{r}\right) $$ Hence for $r>r_s$ and $r_{\rm light} \geq r_{\rm obs}$, $$\left|\frac{dr}{dt}\right|_{\rm light} > \left|\frac{dr}{dt}\right|_{\rm obs}$$ and the light always "catches" the falling observer.

Answer 1

The infalling observer can 'see' whatever events are in its past light cone. The past lightcone of the infalling observer at the point of intersection with the horizon does not enclose the entire exterior region. In fact, no point on the infalling trajectory does, even at the singularity. Therefore the infalling observer unambiguously does not see the "end of the Universe".

Let me summarize my reading of your objection:

1. The infalling observer does not cross the event horizon in finite Schwarzschild time.

2. After infinite Schwarzschild time, all causal lines reach timelike infinity; i.e. they are causally connected to all exterior light signals.

3. Therefore, after infinite Schwarzschild time the infalling observer is causally connected to all infalling light signals; it "sees the end of the Universe".

4. Events themselves are frame-invariant. Therefore, the experience of the infalling observer must be to witness the end of the Universe.

Premise 2 is false. The infalling observer never reaches timelike infinity, either in Schwarzschild time (which fails to paramaterize the entire infalling worldline) or even in proper time: it reaches a point on the the singularity, and that point is not causally connected to all exterior light signals.

Answer 2

Your assertion that in Schwarzschild coordinates "light always catches the observer" is false. There are several flaws in your logic:

1. You are comparing $dr/dt$ at the same value of $r$. This by definintion means that the light has already caught up to the observer by assumption.
2. Even if you did the comparison at fixed $t$, the assertion $$\left|\frac{dr}{dt}\right|_{\rm light} > \left|\frac{dr}{dt}\right|_{\rm obs}$$ does not automatically imply that the light will catch the observer. The obvious counter example is if $r$ is an exponentially decaying function. Suppose that $$ r_\mathrm{obs}= 2+\exp(-t/2)$$ and $$ r_\mathrm{light}= 2+2\exp(-t/2)$$ then $$\left|\frac{dr}{dt}\right|_{\rm light} > \left|\frac{dr}{dt}\right|_{\rm obs}$$ while $$ r_\mathrm{obs} < r_\mathrm{light} $$ for all $t$.

This is more than just a mathematical statement, as the above are approximate solutions of the geodesic equation for massive and massless particles near the horizon.

Edit:

Clarifying the last statement, the equation of motion for a radially infalling geodesic in Schwarzschild black hole can be written:

$$ \frac{dr}{dt} = - \frac{r-r_s}{r}\sqrt{1 + \frac{r-r_s}{r} \frac{\epsilon}{E^2}},$$

where $\epsilon$ is 0 for lightlike geodesics and -1 for timelike geodesics, and $E$ is conserved (Killing) energy of the particle.

Writing $r(t) = r_s + \delta r(t)$, this becomes

$$ \frac{\delta r}{t} = -\frac{\delta r}{r_s} + O(\delta r^2).$$

Hence when close to the horizon both light and the observer's radial motion are governed by the same equation, which has as a general solution:

$$ r \simeq r_s + A \exp(-t/r_s) $$.

Consequently, if once close to the horizon the light start further from the horizon ($A_{light} >A_{obs}$, then the light will never (in coordinate time $t$) catch up to the observer.

Answer 3

Thanks to the answer provided by @mmeent I have derived the limiting circumstances under which a falling observer can be signalled to by a static observer at some distance from the black hole.

It is indeed the case that both the geodesics of inward travelling light and those of a falling observer reduce to equations of the form $$ r_{\rm light} - r_s \simeq A \exp[-t/r_s]$$ $$ r_{\rm falling} - r_s \simeq B \exp[-t /r_s]$$ as $t \rightarrow \infty$ and $r \rightarrow r_s$ in both cases.

The condition then for the light to intercept the falling observer is that $A/B < 1$ as $t \rightarrow \infty$.

This is a bit like Zeno's paradox in that although the light travels faster than the falling observer at all radii, and continually closes the distance, unless the above condition is satisfied it never quite catches up.

I have provided a full derivation of the conditions for (i) a stationary observer that is passed by another observer free-falling from infinity and (ii) the case of two observers, one at rest and the other that freefalls from the position of the first observer.

In both cases there is a maximum amount of (Schwarzschild) coordinate time that can elapse that still allows a signal from the stationary observer to reach a falling observer. Full details can be found in my answer to this question. The results are:

Case (i) $$\Delta t < \ln \left(\frac{4r_s}{r_0 - r_s}\right)r_s + \left( \frac{2}{3}\left(\frac{r_0}{r_s}\right)^{3/2} + 2\left(\frac{r_0}{r_s}\right)^{1/2} - \ln \left| \frac{\sqrt{r_0/r_s} + 1}{\sqrt{r_0/r_s} -1}\right| - \frac{5}{3}\right)r_s - r_0$$ where $r_0$ is the position of the signalling observer (and through which the falling observer passes) and $r_s$ is the Schwarzschild radius.

Case (ii) $$\Delta t < r_s \ln \left(\frac{4r_s}{r_0}\right) + b_{\rm rs} + r_s - r_0$$ where $$b_{\rm rs} = r_s\left(\frac{r_0}{r_s}-1\right)^{1/2} \left( \eta_{\rm rs} + \frac{r_0}{2r_s}(\eta_{\rm rs} + \sin \eta_{\rm rs})\right), $$ $$\eta_{\rm rs} = \cos^{-1}\left(\frac{2r_s}{r_0} -1 \right).$$ The picture below plots these functions for the two cases.