Terminal velocity and distance traveled with constant but limited power

Question

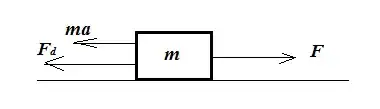
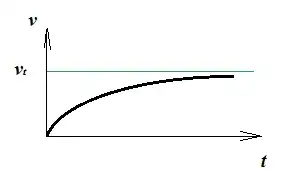
I'm trying to model how far to move an object over time according to a power applied resisted by friction.

So maybe... an object accelerates at a certain rate until the power provided can no longer overcome friction (in relation to mass of the object), causing the object to move at a constant velocity as long as power is still applied (and slow down due to friction once the power stops acting on it). Answering the questions: What the the position, velocity, and acceleration at a certain period of time? After a certain time interval the velocity and acceleration should be constant by these criteria. Also, how is the terminal velocity in this situation determined?

For a real-life example, a car can accelerate over time, up to a certain max speed where the power of the car cannot overcome the force of friction/drag.

All the examples I have found relate to aerodynamic drag, thus the resistance scales with the velocity, though I'm not sure how this would apply in a different case.

Answer 1

If we apply a force $F$ to a mass $m$ and a friction force (drag) $F_d$ also acts on it the force diagram becomes:

With $a$ the acceleration the object experiences, the equation of motion becomes:

$F=ma+F_d$.

As the mass moves towards the right, say for an infinitesimal distance $dx$, an infinitesimal amount of work $dW$ is performed on $m$ by $F$:

$dW=(ma+F_d)dx$.

If we divide both sides with $dt$ then $\frac{dW}{dt}=P$ with $P$ the power, constant in this case. So we have:

$P=\frac{dW}{dt}=(ma+F_d)\frac{dx}{dt}$ and by definition $\frac{dx}{dt}=v$, so:

$P=(ma+F_d)v$.

Now the question becomes, what is $F_d$?

We know that in general $F_d \propto v^n$, where $v$ is the velocity and $n$ is some exponent. For instance in the case Navier Stokes drag (viscous drag of a fluid on a spherical object), $n=1$.

For the case of air drag the exponent $n=2$ is generally assumed.

Let's however explore the case of $n=1$, so that $F_d=kv$, with $k$ a proportionality constant, so we get:

$P=(ma+kv)v$.

With $a=\frac{dv}{dt}$, we get:

$P=mv\frac{dv}{dt}+kv^2$, a differential equation that can be separated by variables to yield:

$m \frac{v}{P-kv^2}dv=dt$.

This can be integrated between $t=0, v=0$ and $t, v$ and yields after reworking:

$\Large{v=\sqrt{\frac{P}{k}(1-e^{-\frac{2kt}{m}})}}$.

For $t \to +\infty$ the exponential term $e^{-\frac{2kt}{m}} \to 0$, so that the terminal velocity $v_t$ is achieved for $t = +\infty$ and is given by:

$\large{v_t=\sqrt{\frac{P}{k}}}$.

Since as the terminal speed is only achieved for $t = \infty$, it will be achieved also only for $x = \infty$.

The general shape of the $(v,t)$ function is as follows, with $v_t$ being reached only asymptotically:

Answer 2

This may not be the ultimate answer as I don't know the quantitative relations between variables. But I can say the following:

The ultimate velocity is determined by the power ($P$) of the car (or other objects, let's use car for example) and the friction ($\mathbf{f}$). Now that $$P=\mathbf{v}\cdot \mathbf{f}$$ It means that all the power of the car is used to overcome the friction to move in a constant speed. Once you know the two parameters, you can get the velocity $\mathbf{v}$ easily.

The acceleration can be calculated from the function of $\mathbf{f}$ over time and the mass of the car ($m$) by $$\mathbf{a}(t)=\left(\frac{P}{v}\mathbf{e}_v-\mathbf{f}\right)/m,$$ where you should know how the friction related to speed and position. $\mathbf{e}_v$ is the direction vector of the velocity $\mathbf{v}$ at time $t$.

The position of the car is just a time integral of velocity, with the velocity is just the time integral of the acceleration. You can calculate them easily if you know the rest of the relationships--especially how the friction relates to velocity and so on. You may get a set of equations to fully solve the problem.

Answer 3

Here are some simple cases applied from How to get distance when acceleration is not constant?

1. Constant Power $P$, Constant Friction $F$ $$ \begin{align} a(v) & = \frac{P}{m v} - \frac{F}{m} = \frac{P}{m} \left( \frac{1}{v} - \frac{1}{v_{final}}\right) \\ v_{final} &= \frac{P}{F} \\ t = \int \limits_{v_1}^v \frac{1}{a(v)}\,{\rm d}v &= \frac{m v_{final}^2}{P} \ln \left( \frac{v_1-v_{final}}{v-v_{final}} \right) - \frac{m v_{final}(v-v_1)}{P} \end{align} $$
2. Constant Power $P$, Linear Friction $F=\alpha v$ $$ \begin{align} a(v) & = \frac{P}{m v} - \frac{\alpha v}{m} = \frac{P}{m} \left( \frac{1}{v} - \frac{v}{v_{final}^2} \right) \\ v_{final} & = \sqrt{\frac{P}{\alpha}} \\ t = \int \limits_{v_1}^v \frac{1}{a(v)}\,{\rm d}v & = \frac{m v_{final}^2}{2 P} \ln \left( \frac{v_1^2-v_{final}^2}{v^2-v_{final}^2} \right) \end{align}$$
3. Constant Power $P$, Air Drag $F=\beta v^2$ $$\begin{aligned} a(v) & = \frac{P}{m v} - \frac{\beta v^2}{m} = \frac{P}{m} \left( \frac{1}{v} - \frac{v^2}{v_{final}^3} \right) \\ v_{final} &= \sqrt[3]{\frac{P}{\beta}} \\ x = \int \limits_{v_1}^v \frac{v}{a(v)}\,{\rm d}v & = \frac{m v_{final}^3}{3 P} \ln \left( \frac{v_{final}^3-v_1^3}{v_{final}^3-v^3} \right) \end{aligned}$$

The velocity profile is too complex for the last case to include in this answer. You are welcome to use Wolfram Alpha to solve the integrals yourself.