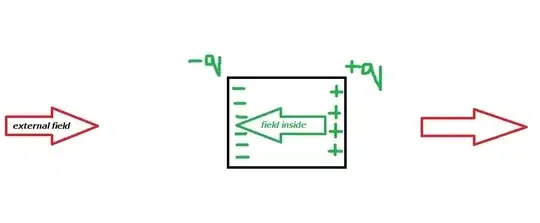
Lets assume that there is an external field +E acting on a conducting plate from left to right. Due to this, some electrons will drift from right to left to cancel out this electric field inside the conductor. But since some electrons have moved to the left surface of the sheet, there should(?) be an accumulation of positive charge on the right side of the sheet which should also have an electric field of its own (will this accumulation of positive charge on the right side of the sheet be equal in magnitude to the charge due to the accumulation of electrons on the left side ?). So how is the net electric field ever getting zero because there will always be some positive charge in the conductor which will have a field of its own. If maybe this field attracts some electrons to neutralize it, there will always be some positive charge due to this attraction of electrons to have a field of its own. Please tell me what exactly happens inside the conductor since my above idea is probably wrong.
I know that "its electrostatics so no field can move and thus field should be zero" but I want to know HOW this happens and no other question addresses this "HOW" or my concern about the positive charge build up (if there is any kind of buildup)
Can a conductor run out of electrons to cancel external electric fields? ^This answer talks about the electrons neutralizing a positive field by drifting to one side but then it loses context to what I want to know by talking about the impact of the external field strength (I want to know the impact of the field created by the positive charge inside the conductor, if there is any)
Why the electric field inside a conductor is zero? ^The answer in this thread talks about the negative charge moving (as i have already mentioned above) but doesn't tell whether there is any kind of positive charge build up on the opposite side and the field due to it (because the electrons have moved to the other side)