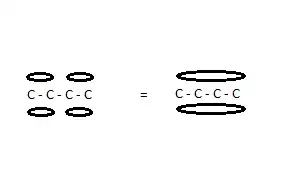Why does the conjugated $\pi$ bond not violate the Pauli Exclusion Principle?

Question

Let's look at the molecule 1,3 butadiene:

$CH_2=CH-CH=CH_2$

and number the carbon atoms 1 to 4 from left to right.

The bonds between 1 and 2 and between 3 and 4 are double bonds: each constitutes a $σ_{2p}$ and a $π$ bond (molecular orbitals). Studies on bond length and chemical reactivity show unequivocally that the two $π$ bonds do not exist separately but that instead the electron clouds merge into one $π$ molecular orbital, extending over the four carbon nuclei.

This link shows the bonds in far better graphical detail.

Both Atomic and Molecular Orbitals normally only contain 2 electrons, with different Spin Quantum Numbers $m_s$, in order to respect the Pauli Exclusion Principle. A third electron in the same AO or MO would immediately violate the Pauli Exclusion Principle because $m_s=\pm\frac{1}{2}$.

The conjugated $π$ bonds in 1,3 butadiene appear to contain 4 electrons though. How is this not a violation of the Pauli Exclusion Principle?

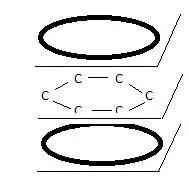
This (perceived?) problem is even ‘worse’ when we look at the structure of benzene ($C_6H_6$) which for a long time was considered to be made up of six single $σ$ bonds (molecular orbitals) and three double bonds ($σ$ and $π$, molecular orbitals). But such a structure could never be a regular hexagon because (all other things being equal) the bond lengths (i.e. inter-nuclear distances) are less for double bonds than for single ones (this is easy to explain based on electrostatic shielding). Benzene turns out to be perfectly hexagonal.

Also, when substituting two adjacent hydrogen atoms with some other atom (a so-called ortho-substitution) one would expect two different ortho compounds to result but this is not the case: there is only one ortho-substitute.

Text books therefore usually represent the benzene structure as below:

Two $π$ rings containing a total of six electrons hovering in molecular orbitals above and below the $C$ plane, forming one single $π$ molecular orbital. Again, assuming these electrons are in the same quantum state, it’s hard to see how this is not a violation of the Pauli Exclusion Principle.

Answer 1

Just a chemist, but maybe there would've been less confusion in that forum. It's because this is not how the model works. Orbitals are something you get from Hartree-Fock theory (let's leave it at that). Here is how it works in principal, mind you that this is just a model:

Let's take Benzene as an example. You have those atomic orbitals from which you form your molecular orbitals. Take hydrogen: You have one electron from each atom in an s orbital. If you combine them, you get two combinations, one anti-bonding and one bonding. Two atomic orbitals yield two molecular orbitals. The two electrons will sit in that occupied orbital.

Now coming back to benzene: The so-called pi orbitals form from atomic p-orbitals sitting on top of the carbon atoms in the benzene. You can imagine that each carbon gives you one electron in that p orbital to obtain the 6 electrons that according to you occupy that pi orbital. From them you obtain 6 molecular orbitals. Three of them will be occupied with 2 electrons each and 3 will remain empty. There is no violation.

So in short, your mistake is thinking there was only one pi orbital when in fact there are 3 for benzene and 2 for butadiene.

Answer 2

The reason is that also other orbitals are occupied. For example for benzene using the hückel-method you will find following molecular orbitals. The three lowest lying are occupied because of the 6 electrons. The pauli exclusion principle cannot be violated!