Would particles behave the same way as a satellite orbiting earth, only far more compact and rapid correlating to the gravitational force of the black hole?
Asked
Active
Viewed 251 times
2 Answers
4
Let's assume we are dealing with circular orbits for simplicity. In that case the orbital velocity for a satellite at a distance $r$ from a black hole is given by:
$$ v = \sqrt{\frac{GM}{r - r_s}} \tag{1} $$
where $r_s$ is the radius of the event horizon:
$$ r_s = \frac{2GM}{c^2} \tag{2} $$
Now let's rearrange equation (2) to get:
$$ GM = \frac{c^2r_s}{2} $$
then substitute this into equation (1) to get (after a bit of rearrangement):
$$ v = c\sqrt{\frac{r_s}{2(r - r_s)}} \tag{3} $$
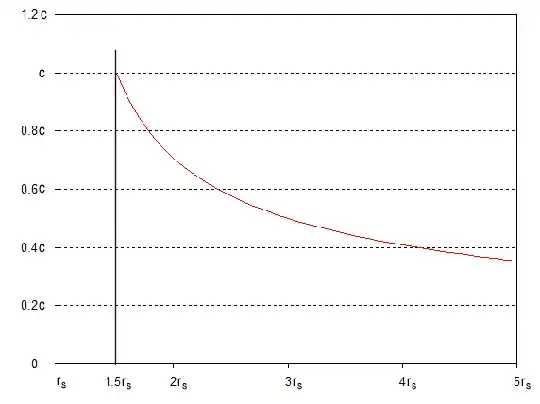
Now let's have a look at the graph of how $v$ varies with $r/r_s$:
What we find is that at $r = 1.5r_s$, which is still outside the event horizon, the orbital speed reaches the speed of light, $c$. This value of $r$ is called the photon sphere because it's the point at which light will orbit the black hole.
We know nothing can move faster than light, so nothing can have a stable circular orbit for $r < 1.5r_s$. While it's true, as Omry says, that you can't have any stable orbits inside the event horizon you can't even have stable orbits outside the event horizon if your distance from the centre of the black hole is less than $1.5r_s$.
Actually it's even worse than that. For a massive particle, i.e. some particle that unlike a photon has a rest mass greater than zero, the lower limit for a stable orbit is $r \ge 3r_s$. So a satellite can have no stable orbit round a black hole even while it's quite a way outside the event horizon.
John Rennie
- 367,598
1
No, they do not stay in constant orbit.
Anything that enters a black hole must reach the singularity, and it will do so by constantly reducing its distance from it.
(Think of it this way: If you've entered a black hole, your escape speed is larger than the speed of light, so one cannot possibly expect that you would remain in orbit inside it)
Omry
- 1,355