How fast do electrons travel in an atomic orbital?

Question

I am wondering how fast electrons travel inside of atomic electron orbitals. Surely there is a range of speeds? Is there a minimum speed? I am not asking about electron movement through a conductor.

Answer 1

The state of an electron (or electrons) in the atoms isn't an eigenstate of the velocity (or speed) operator, so the speed isn't sharply determined. However, it's very interesting to make an order-of-magnitude estimate of the speed of electrons in the Hydrogen atom (and it's similar for other atoms).

The speed $v$ satisfies $$ \frac{mv^2}2\sim \frac{e^2}{4\pi\epsilon_0 r}, \qquad mv\sim \frac{\hbar}{r} $$ The first condition is a virial theorem – the kinetic and potential energies are comparable - while the second is the uncertainty principle. The second one tells you $r\sim \hbar / mv$ which can be substituted to the first one (elimination of $r$) to get (let's ignore $1/2$) $$ mv^2 \sim \frac{e^2 \cdot mv}{4\pi\epsilon_0\hbar},\qquad v \sim \frac{e^2}{4\pi\epsilon_0\hbar c} c = \alpha c $$ so $v/c$, the speed in the units of the speed of light, is equal to the fine-structure constant $\alpha$, approximately $1/137.036$. The smallness of this speed is why the non-relativistic approximation to the Hydrogen atom is so good (although a non relativistic kinetic energy was assumed from the start): the relativistic corrections are suppressed by higher powers of the fine-structure constant!

One could discuss how the speed of inner-shell electrons and valence electrons is scaling with $Z$ etc. But the speed $v\sim \alpha c$ would still be the key factor in the formula for the speed.

Answer 2

This is the realm of quantum mechanics and classical notions about point like electrons travelling at certain speeds don't really apply in this domain. So there isn't an average speed or a minimum speed or even a maximum speed (except for the speed of light which is the maximum speed for any particle with mass).

The closest you can come to having any concept of speed for an electron in an orbital would be to apply the Heisenberg uncertainty relation which states that $$\Delta x \Delta p \geqslant \hbar$$ So if you plug the size of the orbital in for $\Delta x $ and solve for $ \Delta p $ you would have an estimate for the uncertainty in the momentum which you could then relate to the uncertainty in speed.

Answer 3

I think it may be helpful to fill out the answer to this question by summarizing what happens for inner electrons.

We take as starting point a nucleus with charge $Z$ with just a single electron bound to it. Note, for $Z > 1$ this would not be a neutral atom but it is a useful starting point for the calculation. In this case one finds, from non-relativistic quantum theory, that the mean value of the kinetic energy of the electron in the ground state is equal to $$ \left< {\rm KE} \right> = \frac{1}{2} m (Z \alpha)^2 c^2 $$ where $\alpha = e^2/4\pi \epsilon_0 \hbar c$ is the fine structure constant, whose numerical value is about $1/137$. So on this basis we may say that the r.m.s. speed of the electron in the ground state of such a charged atom (ion) is $$ v_{\rm r.m.s.} = Z \alpha c. $$ (You can also think of this as the r.m.s. momentum divided by the mass $m$).

Now let's consider neutral atoms. The above calculation gives a rough order-of-magnitude estimate if we replace $Z$ by $Z-\sigma_n$ where $\sigma_n$ is a screening factor which accounts for the fact that an electron in shell $n$ (i.e. having principal quantum number $n$) does not, on average, experience the whole electric field of the nucleus, but a reduced electric field owing to the presence of the negative charge of the other electrons. For the outermost shell this $\sigma_n$ will be about $Z-g/2$ where $g$ is the number of electrons in the outermost shell (equal to the group number in many cases). The idea is that all the electrons in lower shells shield the nuclear charge, and each of those in the final shell shield it about half the time for the other electrons in the same shell. All this is just a rough statement which ignores the effects of the shape of the orbitals. It leads to an order-of-magnitude estimate of the r.m.s. speed of the outermost electrons: $$ v_{\rm outer} \approx \frac{g \alpha c}{2} $$ Note, we have ignored the fact that the wavefunction itself is different for $n > 1$ compared to $n=1$, so there will be further factors relating to $n$.

Proceeding now to inner shells, one can take as $\sigma_n$ approximately the number of electrons in the shells at or lower than the one you are thinking about. For shell $n$ this number is $2 n^2$. So then we get $$ v_{\rm inner} \approx (Z - 2 n^2) \alpha c. $$

One thus finds that for uranium ($Z = 92$) the speeds for the inner-most shell are of the order of the speed of light. This makes this atom a useful test-bed for relativistic quantum theory. More widely, from caesium $(Z = 55)$ on up the inner electrons have speeds of the order of half the speed of light, and from francium $(Z=87)$ about half the electrons have speeds above a third of $c$.

Altogether, then, fast electrons are a significant feature of the atomic physics of heavy elements. (And for precision calculations one must allow for relativistic effects in every case, not just the high $Z$ atoms).

Answer 4

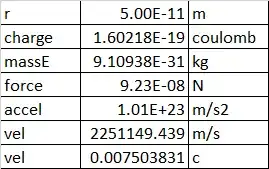
This sounds absurdly simple, but for order of magnitude results, it matches well with online results and other results here. People tend to think that good old Newtonian dynamics are useless on the atomic scale, but they still apply if the velocity is well below light speed.

Simply take the electric force between the electron and nucleus, convert it to an acceleration by a = F/m, and then balance that acceleration with centripetal acceleration of velocity squared over r. That is, v = SQRT(rF/m).

I know, you might say that doesn't work, an electron is not like a satellite at a point location, but is rather smeared out in an electron cloud about an orbital. But remember - the definition of the orbital is a path at which each point is a balance between kinetic and potential energies. So each location on a spherical orbital has to be a point of balance between centripetal acceleration and electrostatic attraction.

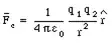where epsilon-zero is 0.00000000000885 and the charge q of an electron is 1.606e-19 coulomb.

Hydrogen example: