If a lens focuses all incoming light to a point, how do we get 2D images?

Question

How do lenses produce 2-dimensional images, if a lens bends all incoming rays of light to intersect at the focal point? Shouldn't this produce a single dot of light on a screen placed at the focal length?

This is basically the standard diagram that always shows up in textbooks:

I know this doesn't happen in real life--I used to use telescopes pretty frequently for work. The most in-focus image would be the one with the smallest diameters for the stars, which, of course, we think of point sources at infinity. But--the light from all stars (despite being at infinity) is not all focused at a single point. Instead, each star's light is focused at its own $(x,y)$ point on a 2D image.

I can't reconcile the theory as I understand it with any of my real-life experience with optics. What am I missing?

Answer 1

...if a lens bends all incoming rays of light to intersect at the focal point? Shouldn't this produce a single dot of light...?

(In your diagram, the source image is at infinity. I will continue the analysis along that idea.)

It is true that all rays parallel to the axis focus to that single dot. Not all rays, however, are parallel to the axis:

Rays coming from different angles focus to different points. That is how an image is formed.

Answer 2

A convex lens does not focus all the rays to a single point. It focuses the all axis parallel rays on the focal point. It also focuses all the rays emanating from a given point to a corresponding point on the other side. That point is the image of the original point.

The standard diagram shows that a lens sends all axis parallel incoming rays to the focal point. Parallel rays can be thought of as emanating from a point at inifinity. So you can think of focal point as the image of a point at infinity.

More general ray diagrams look like this:

The full rules for drawing ray diagrams as given in the Hyperphysics article on the subject:

1. A ray from the top of the object proceeding parallel to the centerline perpendicular to the lens. Beyond the lens, it will pass through the principal focal point. For a negative lens, it will proceed from the lens as if it emanated from the focal point on the near side of the lens.
2. A ray through the center of the lens, which will be undeflected. (Actually, it will be jogged downward on the near side of the lens and back up on the exit side of the lens, but the resulting slight offset is neglected for thin lenses.)
3. A ray through the principal focal point on the near side of the lens. It will proceed parallel to the centerline upon exit from the lens. The third ray is not really needed, since the first two locate the image.

Answer 3

Your diagram shows parallel light beams originating from infinity. Light entering the eye in the real world isn't all parallel.

In the real world, all the light that bounces off a single point will hit the sensor (eye-cone, digital sensor, etc) at a single point, assuming that point is in focus. However, light from different points will strike the sensor at different places, creating the image that you see.

If the point is not in focus, it will be spread out on the sensor in a circle. Photographers call this the circle of confusion.

Playing around with this tool should make it pretty obvious. I took these images from my answer to the Photography.SE question How does aperture work without “cropping” the image hitting the sensor?

Answer 4

Truth be told: geometric optics is wrong. It is sufficient for small angles and not too complicated setups, but is still an approximation.

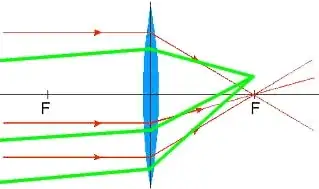
The first thing: Normal lenses do have not a focal point, but something which resembles more a line, the so-called caustic. The correct shape for getting a perfect point on the line crossing the middle of the lens (I call that axis now) is not a spherical shape, but a complicated curve, the cartesian ovoid. So you won't get a point image from normal optical surfaces in the first place; there are aplanatic lenses, but they are extremely expensive.

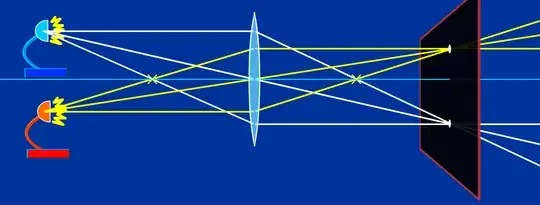
Second: Even if you have an aplanatic lens, still light is not a ray, but a wavefront. A perfect planar wavefront which passes an aplanatic lens forms still not a point, but a so-called airy disc. You see that very well that if you increase magnification; at some point the image gets more and more fuzzy, the airy discs of the point images are starting to overlap and ruin the image. The only possibility to avoid that is to increase the size of the lens or mirror which makes the airy disc smaller (That is the reason astronomers need big, big lenses and mirrors).

But even that is not sufficient enough if you want really high-quality, in that case you need the exact light equations which are described by the Maxwell equations.

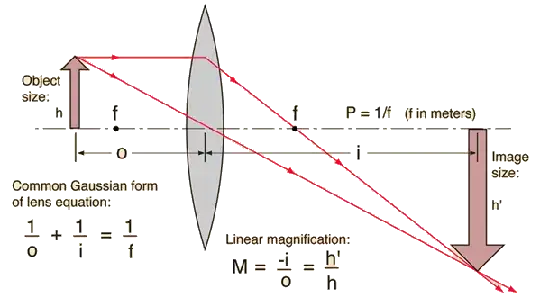
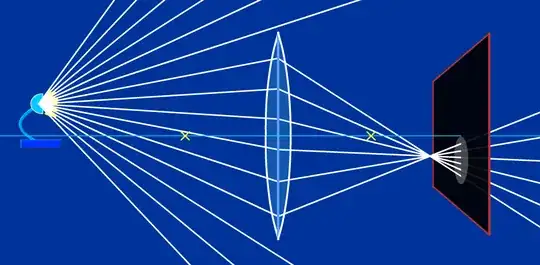
Now we need an image, I am using the open source image of the German Wikipedia under "Linsengleichung":

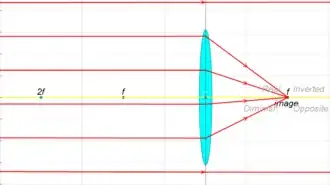
As you see, if the source of the light rays is near the lens, the rays are not running parallel and their image does not develop in the focal point f, but in increased distance. You are using two rays from the same point: One parallel to the axis which crosses the focal point and one which runs from the point exactly through the lens. Where they cross is the image of the source point and this is not the focal point !

Answer 5

There is a fallacy in your question which might be the source of your confusion. It is not all light that gets focused to a point, it is only rays parallel to the lens axis!
For the case of two (point source) stars, if the rays of one star are parallel to the lens axis, the rays of the other star will not be (not co-linear), therefore its image will appear at a different point than the first star.