How are images in a telescope finite rather than just a point?

Question

I understand that light passed through the objective lens of the telescope produce an image that is real and inverted, and have a height which is measured as the distance between the focal point and the principal axis, but my question is: Why? If all the light is concentrated onto the focal point, then why does the height matter, because wouldn't the light rays coming from a given object be focused on to a single point? Please help me understand the lapses in my logic.

Thanks for any help you can give me, I really appreciate it!

Answer 1

The lens does not have a single focal point.

For an ideal lens focused at infinity, all the light that enters the lens parallel to the main axis will be focused to a single point. But light that enters at a different angle will be focused onto a different point.

Because light from an extended object will reach the lens via different angles, the different portions of the object will be mapped onto different portions on the focal plane.

From https://commons.wikimedia.org/wiki/File:Focalisation_lentille.png

In the above image, light entering parallel to the main axis is shown as the green column. That light is brought to a focus at $F$. While the light entering at a specific angle to the main axis (in red) comes to a focus at $F'$.

Answer 2

First of all, your definition of height is unclear to me. I'm assuming by height you mean the separation from the optical axis of the image of a point object through the objective.

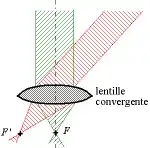
One way of looking at this is that for an object infinitely far away and the light from which arrives at the objective at a non-zero angle with respect to the optical axis, the "height" of the object is also "infinite", so the image rendered has a finite height rather than zero.

Now suppose the object with height $h_o$ is a distance $x_o$ away from the objective, and its image forms at $x_i$ with height $h_i$. If the rays from the object reach the objective at an angle $\theta_o$, we have $$h_o = \tan(\theta_o)x_o. $$ For an object very far away, we have $$x_i \approx f$$ where $f$ is the focal length of the objective. The linear magnification is the negative ratio of distances of the image and the object to the objective: $$ M = -\frac{x_i}{x_o} $$ so the height of the image is $$ h_i = M h_o = -\frac{x_i}{x_o} h_o = -\frac{x_i}{x_o}\tan(\theta_o)x_o = -\tan(\theta_o) x_i \approx -\tan(\theta_0)f $$ where the negative sign indicates that the image is inverted. This relation can also be seen by simply drawing rays from the object, without doing math.

Answer 3

Light cannot be focused to dimensions smaller than about its wavelength. A point will be imaged into a point spread function, which for an ideal circular lens has a dimension of $1.22 \lambda / NA$. If you search for point spread function you will learn the details.