Modern atomic clocks only use caesium atoms as oscillators. Why don't we use other atoms for this role?
5 Answers
"Because that is how the second is defined" is nice - but that immediately leads us to the question "why did Cesium become the standard"?
To answer that we have to look at the principle of an atomic clock: you look at the frequency of the hyperfine transition - a splitting of energy levels caused by the magnetic field of the nucleus. For this to work you need:
- an atom that can easily be vaporized at a low temperature (in solids, Pauli exclusion principle causes line broadening; in hot gases, Doppler broadening comes into play)
- an atom with a magnetic field (for the electron - field interaction): odd number of protons/neutrons
- an atom with just one stable isotope (so you don't have to purify it, and don't get multiple lines)
- a high frequency for the transition (more accurate measurement in shorter time)
When you put all the possible candidate elements against this table, you find that Cs-133 is your top candidate. Which made it the preferred element; then the standard; and now, pretty much the only one used.
I found much of this information at http://www.thenakedscientists.com/forum/index.php?topic=12732.0
- 119,981
The choice of cesium is due to various factors. It's worth noting that your statement "Modern atomic clocks only use caesium atoms" is simply untrue. At the very least, rubidium and hydrogen clocks are common, and you can get rubidium standards on eBay for well under $200. But the best performance comes from using cesium. In part this is because it was chosen as the standard, and as such it is considered more useful to spend development effort on improvements to the standard rather than an alternative.
But why was cesium chosen? Various factors:
At reasonable temperatures, cesium has a high vapor pressure, making resonance effects relatively easy to observe.
Large hyperfine transition, creating better Q of the resulting resonator.
As opposed to rubidium, cesium only has one stable isotope, so getting a really pure gas is much easier. No isotopic separation required.
EDIT - PlasmaHH has remarked on the superior frequency stability of hydrogen over cesium. While this is true, cesium shows better intrinsic accuracy (about 2 orders of magnintude), and no ageing effects, where hydrogen does age. The combination makes cesium a better standard, since a standard has no reference to check against in order to calibrate out drifts. See http://www.chronos.co.uk/files/pdfs/itsf/2007/workshop/ITSF_workshop_Prim_Ref_Clocks_Garvey_2007.pdf for a discussion by a manufacturer.
- 6,460
As mentioned by WhatRoughBeast, caesium offers several advantage over other microwave standards. Its most important feature is the presence of an atomic transition with a very small linewidth. This allows the energy of this transition to be established very accurately (see the uncertainty principle).
However, caesium is not the only atom with a narrow transition. For example, Yb+ ions have an octupole transition that is nHz wide: an atom excited to this state would last for several years before it decayed. This, in principle, would allow the frequency of the transition to be determined extremely well.
So why do atomic clocks only use caesium? Well...
They don't
The modern second is defined in terms of the Cs hyper-fine transition so, of course, no other clock can be as accurate as caesium, purely by definition. But in the field of atomic clocks, the word "accurate" takes on a specific meaning.
Frequently in physics, we refer to accuracy and precision. The accuracy of something is how well its average agrees with the "correct" value, whereas the precision is how scattered the results are. See the image below.
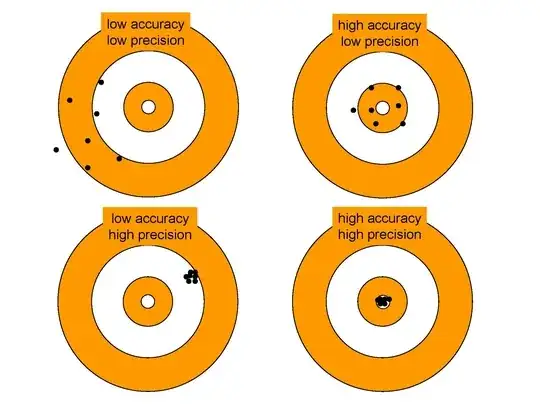
For atomic clocks, the relevant quantities are accuracy and stability. Here, the accuracy refers to how well the clock realises the SI second and the stability refers to how quickly it does so. The (in)stability of a clock occurs because all measurements have some statistical noise on them: it's only after many measurements that you get the right answer, and the stability tells you how many measurements you need to make.
Secondary representations of the SI second
So if the second is defined by caesium, why did I say that not all clocks use it?
The Comite International des Poids et Mesures (CIPM) in 2012 adopted 8 secondary representations of the SI second. 7 of these are optical clocks which offer many advantages over a caesium fountain (known as a microwave standard).
To know how good a clock is, you must compare it against another clock otherwise you have no reference! The best modern caesium fountains agree with each other to approximately $\frac{\Delta \nu}{\nu} \approx 10^{-16}$. Modern optical atomic clocks, such as ytterbium ion clocks or strontium lattice clocks, can exhibit agreements approaching $\frac{\Delta \nu}{\nu} \approx 10^{-18}$: that's 100 times better! Moreover, optical clocks are still improving quickly. It seems that, very soon, the best optical clocks will outpace microwave clocks by many orders of magnitude. See this article in Nature for more information.
These clocks work by using transitions that use visible frequencies, as opposed to microwave frequencies used in Cs clocks. So, while Cs still is the definition of the second, modern optical clocks offer far better performance and are expected to soon replace caesium as the standard.
The graph below shows the performance of atomic clocks throughout time. The red points represent the points at which optical clocks are performing better than caesium clocks. It is important to notice that caesium fountains have experienced improvements of 5 orders of magnitude over the last 40 years: no mean feat!

- 137,480
- 753
Because one second is defined as (from the SI brochure):
the duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom, ${}^{133}\mathrm{Cs}$.
Thus, using any other atom is irrelevant (even if calculate some correction time factor).
- 137,480
- 1,009
As other users have said, it has one stable isotope, so that's nice.
It's also the SI standard. We define the second by Caesium. Specifically:
The second is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom.
So, if we were to use another atom, it would not be as precise. Even if we calculated how many periods of another substance it took to equal a second, even if it was only off by a factor of 10-12 , it'd still be not as accurate as the system we're using today.