Entanglement between the electrons in the Laughlin wave function

Question

Consider the $1/3$-Laughlin wave function

$$ \Psi \propto \exp \left(-\sum_i |z_i|^2 \right) \prod_{1\leq i<j\leq N} (z_i-z_j)^3 . $$

It cannot be written in the form of a Slater determinant, which means, the electrons are entangled somehow. I tried to quantity the entanglement between them using the geometric approach, i.e., finding its best Slater approximation (maximizing the overlap $\langle \Psi|\Psi_{slater}\rangle $) and using the maximum value $I_{max}$ of the overlap as a measure. It turns out that there is almost a linear relationship between $N$ and $\ln(I_{max})$:

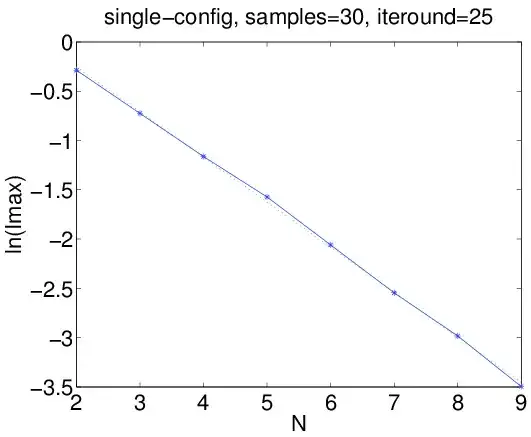
But does this mean anything? Why is there no crossover regime at the $N\rightarrow 0 $ limit?

Answer 1

This is interesting! Just want to ask a few questions for clarification: (1) Which geometry did you use for the states? disk, sphere, torus? (2) Which set of Slater determinants did you computed overlaps with? for example, did you use a fixed single particle basis and did the optimization over occupation numbers only, or did you allow for changes of the single particle basis? (3) Did make sure you held the Laughlin state with the same constant normalization (i.e. norm 1) at each system size? PS: sorry for asking for clarifications in the answers spot, but apparently my "low reputation" does not allow me to make comments.