I'm trying to understand the difference between proper distance $d\sigma$ and coordinate distance $dr$ in Schwarzschild geometry. The bottom bit of the diagram represents flat space, the upper bit curved space. The inner circles represent Euclidean spheres of radius $r$, the outer circles radius $r+dr$.
Is the proper radius of these circles the same as $r$? I think I mean if I measured the radius of these circles with a real ruler would I get the coordinate distance $r$ of the Schwarzschild metric?
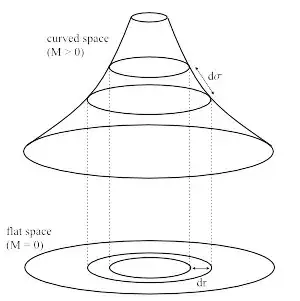
The more I think about this the more confusing I find it.