The wavefunction for an electron within a hydrogen atom in the $2s$ state has the following wavefunction:
$$\psi(r,\phi,\theta)=\psi(r)=\frac{1}{2\sqrt{\pi}}\left(2-\frac{r}{a_0}\right)\frac{e^{-r/2a_0}}{(2a_0)^{3/2}}$$
However, at $r=0$,
$$\psi^*\psi\left.\right|_{r=0}=\left(\frac{1}{2\sqrt{\pi}}\left(2-\frac{0}{a_0}\right)\frac{e^{-0/2a_0}}{(2a_0)^{3/2}}\right)^2=\frac{1}{\pi(2a_0)^{3}}$$
I don't understand how this should be possible. My answer doesn't match logic and it doesn't match graphs that I find online. (every graph I see goes to zero at $r=0$)
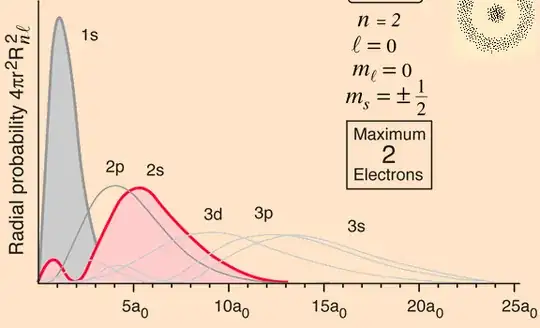
However, this does seem to really be the wavefunction for the 2s state.
Where have I gone wrong?