Energy is actually the momentum in the direction of time?

Question

By comparatively examining the operators

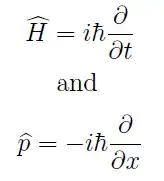
a student concludes that `Energy is actually the momentum in the direction of time.' Is this student right? Could he be wrong?

Answer 1

The student is right in that energy is the analog of momentum in the "time direction" but I wouldn't go so far as to call it "momentum in the direction of time".

It's analogous in two ways that I can think of off the top of my head:

1. It is the time-component of the 4-dimensional energy-momentum vector in special relativity.
2. Noether's theorem relates a symmetry in the laws of physics with respect to a coordinate to a conserved quantity. Momentum is conserved because the laws of physics are invariant with respect to translations in space, and Energy is conserved because the laws of physics are unchanging in time.

I wouldn't call it "momentum in the direction of time" because that phrase, at least to me, implies that energy is more momentum-like than it really is.

Answer 2

Energy is very momentum-like in Relativity theory. For a photon, which has zero rest mass, its energy is the absolute value of its momentum. But not for the reason your student puts forward. What your student said has to be reinterpreted quite a bit.

The first technicality, and it is important, is that $H$ does not equal the operator the student wrote down. In QM, $i\partial\over \partial t$ is not an operator. Whenever you say « operator », you have to be clear in your mind on what space are you operating? The Hamiltonian is an operator in the space of functions of $x$, such as $e^{-x^2}$. An example of $H$ is what was suggested in one of the comments, $-{\partial^2\over\partial x^2}$.
Obviously if you apply your students operator to $e^{-x^2}$, you get zero.

What your student is getting confused by is the difference between a parameter and a variable. The time-dependent Schroedinger equation is better written this way: if $\psi_t(x)$ is the wave function of a system at time t, then it satisfies $$i{d\psi_t\over dt}= H\cdot \psi_t$$ and $\psi_t$ is being treated like a vector which moves with time, so a path in space. For example, $\psi_t (x) = e^{-{x^2\over t}}$ which describes a path which does not satisfy this equation.

Even better would be $$\psi_t = e^{itH}\cdot\psi_o$$ which makes it totally clear that $t$ is a parameter.

But what your student is getting right is the idea that since in relativity time is analogous to space, then motion along the path ought to be analogous to motion in space. The value of any $f(x+a)$ can be found by Taylor's theorem from the value at $f(x)$ and all its derivatives, and this calculus fact can be rewritten in operator terms as $$f(x+a)=e^{a{\partial\over\partial x}}\cdot f.$$ Since this translation in space of a wave function uses the momentum operator of QM in the same way as Schroedinger's equation for time-translation along the path of the wave function uses the operator $H$, (the correct one, not the student's one), the Hamiltonian, which is the energy, we have

translation in space <-----> exponentiation of the momentum operator

translation in time <-----> exponentiation of the energy operator

and so from this we can draw the conclusion that energy is the time-component of momentum.

So in a way, your student was on to something. But one mustn't write $H = i{\partial\over\partial t}$ an equality of operators. That $H\cdot f = i{\partial\over\partial t}\cdot f$ is a condition on $f$ that $f$ has to satisfy.

Answer 3

Here is another way of looking at it, using classical mechanics:

Given a Hamiltonian that may depend explicitly on time: $H = H(q,p,t)$, $(q,p)\in\mathbb{R}^{2n}$. We enlarge phase space to $(Q,P)\in\mathbb{R}^{2n+2}$, $Q=(q,q_e)$, $P = (p,p_e)$. Introduce the corresponding new Hamiltonian $K(Q,P) = H(q,p,p_e) - q_e$. Hamilton's equations of motion now become

$$ \dot{q} = \frac{\partial H}{\partial p} , \quad \dot{p} = - \frac{\partial H}{\partial q}, \quad \dot{q_e} = \frac{\partial H}{\partial t}, \quad \dot{p_e} = 1. $$

These are the original equations of motion for $(q,p)$ in addition to two extra equations. If we recall that in Hamiltonian mechanics $\dot{E} = \partial H/\partial t$, we see the following: The extended system has the energy of the original system as a degree of freedom $E(t) = q_e(t)$, and time as well: $t = p_e$.

In this way, it is natural to think of time as the conjugate of energy.

So yes, even if the wording of the student was imprecise, time and energy are conjugate variables.

Answer 4

In quantum mechanics, the operators work like extractors. They extract physical information from the wave functions for example moment or energy. So they do not carry physical information like direction themselves.