Let a small pressure-sensing device be suspended inside a fluid-filled vessel. ... We find by experiment that at a given point in a fluid at rest, the pressure has the same value no matter how the pressure sensor is placed.
Why is it so?
Asked
Active
Viewed 85 times
1
2 Answers
2
Suppose we had a fluid where the pressure depended on direction:
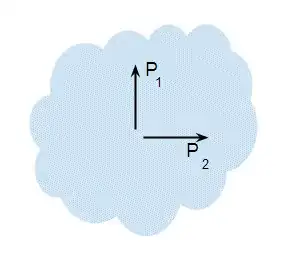
For the sake of argument let's suppose that $P_1 > P_2$. In that case we could take a tube with one end normal to direction $1$ and the other normal to direction $2$:
Because the pressure at the ends is different, fluid will flow round the tube and we have a perpetual motion device. Or rather, the fluid would flow until the pressures equalised and $P_1 = P_2$. But the tube is just a conceptual aid, and we can take it away:
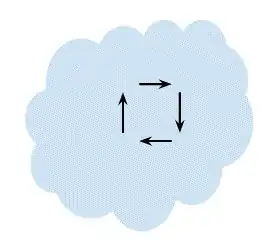
In this case fluid would simply flow in the cycle shown until the pressures equalised. So in any fluid that can flow freely the pressure $P_1$ must equal $P_2$. The argument applies to any directions, and the conclusion is that the pressure must be independant of direction.
There are possible exceptions. For example some structured fluids are anisotropic and may have different viscosity in different directions, or may have an anisotropic yield stress. In these cases it could be the case that the pressure would not be the same in all directions. But then, as Sofia says in a comment, the equations of motion for such a fluid would not be spherically symmetric.
John Rennie
- 367,598
1
In some circumstances, like that of homogeneous and isotropic fluids, the pressure can be described by a tensor which, by the said symmetries, becomes a scalar multiple of the "identity tensor". Such scalar is precisely $p$, the pressure (the tensor is more generally known as stress tensor, and the pressures are its "diagonal components").
Phoenix87
- 9,759