Thank you for our discussion; as indicated and for simplicity, I'll avoid introducing tensors. We can get along fine by treating the pressure as a scalar, a directionless property of any point in the fluid. If a surface—such as a container wall—is introduced, then the pressure corresponds to a force per unit area. That force is a vector acting normal to the surface, and the area can also be treated as a vector through its surface normal. The ratio produces the scalar pressure, as discussed in the links above (example; example; example).
Ultimately, I think you may be looking for something like the following:
To set this up, it's important to address a problem in the question's chain of reasoning. It arises within
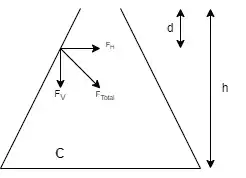
(1) "So even if a point is just vertically downward [from a container wall], it still experiences a pressure of ρgh (with fluid density ρ), even though the fluid above doesn't have a height of h."
and
(2) "The pressure gets contributed due to the vertical component of the normal force by the walls of the container."
and
(3) "the pressure exerted vertically by the wall vertically above C should be ρgd."
Statement (1) is correct. Both the weight of the fluid and the constraint of the container act to produce the pressure field $P = \rho gh$.
Statement (2) starts to become misleading. Pressure is applied by the container wall's normal force in its entirety—both horizontal and vertical components. For a wall region of area $A$, one could resolve the normal force $F = PA$ into the components $F \sin \theta$ and $F \cos \theta$ (with wall angle $\theta$). However, it would be incorrect to say that any arbitrary fluid region below is acted on by only the vertical component. Instead, a small fluid region next to the wall is acted on by the entire force $F$, in addition to fluid forces from all other directions. A small fluid region away from the wall is acted on by forces in all directions from the surrounding fluid. In both cases, the entire set of forces in all directions makes up the pressure field in that region. In no case does either $F \sin \theta$ or $F \cos \theta$ alone act on any arbitrary fluid region.
For these reasons, statement (3) is also potentially misleading. We can't select only the vertical (or horizontal) component of the wall force and follow it vertically (or horizontally) to some other arbitrary part of the fluid and say that only that component applies a pressure. The problem with saying "pressure induced vertically" is evident from the question; we then could just as well say "pressure induced horizontally," and then there's the potential tendency to try to add these two pressures or to combine them like vectors, which is invalid. The wall plays a part in inducing a directionless pressure $P=\rho g h$ everywhere in the fluid. It does this by applying an inward force perpendicular to the wall's surface.
We often hear statements like "The pressure in a fluid corresponds to the weight of the fluid above it." This is true in a sense, but it as well can be misleading because it leads to the misconception that pressure can only act downward, or that forces are transmitted downward only. Instead, pressure arises from forces acting on all sides; if any direction were missing, the water would start to flow spontaneously (as discussed and illustrated in the links above) and wouldn't stop until forces did act on all sides.
So for now, I recommend resisting the tendency to say that pressure is applied in a certain direction, unless you're referring to a certain area $A$ and the corresponding force perpendicular to that area. If you catch yourself saying that pressure is applied vertically (or in any direction), then force yourself to draw the corresponding area—which for a vertical force would be a section of a horizontal plane. In this case, there's no horizontal plane present in the sloping container walls, which is an indication that those walls can't apply a vertical force alone.
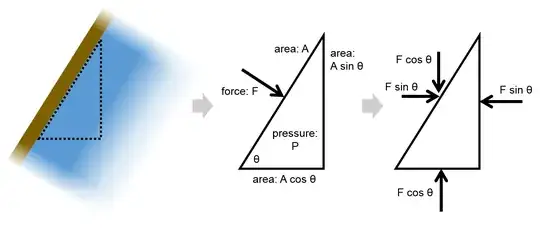
OK, now to the figure above. If you're familiar with free-body diagrams, you can draw a free-body diagram of any conceptual region of a fluid and consider the forces acting on its boundaries, even if sloped (example). The figure shows (left) a 2D visualization of a container wall holding in a fluid; (center) a schematic of the relevant geometry, with trigonometry used to determine the boundary surface areas; and (right) a true free-body diagram of the forces acting on the fluid parcel, with the wall's normal force resolved into horizontal and vertical components. The region is small enough that the weight is negligible and the vertical positions are all essentially at the same depth. For dimensional consistency with the real 3D world, assume that all images show a region with unit depth into the screen.
Since the fluid is at equilibrium, the components of the wall force need to be counteracted by equal and opposite forces applied by the surrounding fluid on the other boundaries. These forces are specific to the boundaries drawn here, and association of the pressure with a force requires consideration of the boundary orientation and its area. Consistent over all three boundaries, the pressure is $\frac{F}{A}=\frac{F\cos\theta}{A\cos\theta}=\frac{F\sin\theta}{A\sin\theta}=P$. It can now be appropriate to associate the pressure with the vertical force $F\cos\theta$ because we've explicitly defined a surface—and that surface in this case has an area of $A\cos\theta$ because the conceptual fluid region is a right triangle (in 3D, a right triangular prism) with hypotenuse corresponding to area $A$.
What if we consider a region farther down (but again small, and still at are same approximate depth, so the weight and pressure variation with depth is still negligible)?
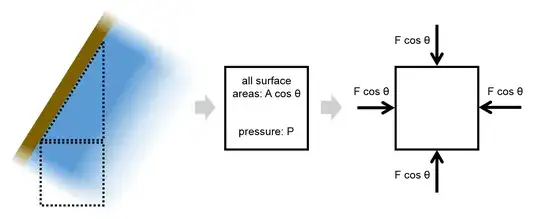
On the upper surface (with area $A\cos\theta$), Newton's third law tells us that the applied force must be equal and opposite to the force on the downward surface of the right triangle, which is $F\cos\theta$. In fact, the forces on all sides must be $F\cos\theta$ to maintain a pressure of $\frac{F\cos\theta}{A\cos\theta}=P$.
But we could just as well have drawn a region with arbitrary surface areas $A^\prime$:
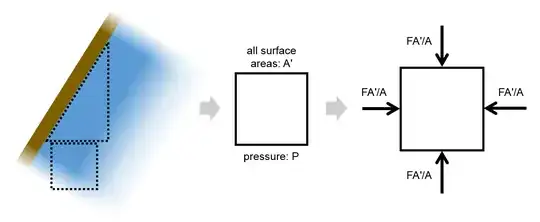
To maintain the pressure $P$ at the same approximate depth, the side forces are now $FA^\prime/A$. Importantly, the $\cos\theta$ factor that arose when finding the vector components of the original wall force $F$ has disappeared. It was applicable only for the right-triangle geometry adjacent to the wall. Thus, $F\cos\theta$ is not a general factor that applies to other arbitrary fluid regions.
I believe this resolves the issue in which it may have appeared that the pressure must be different in different directions; the confusion might have arisen because of the problems, emphasized above, that arise when (1) ascribing a direction to pressure—along with corresponding forces—without defining a suitable corresponding area, and then (2) trying to combine these apparent directional components as if they're vectors when they aren't.