When solving the Einstein field equations in Schwarzschild metric for an observer falling into a black hole the radial coordinate r of the black hole and time t switch roles in the equations when r<2M.
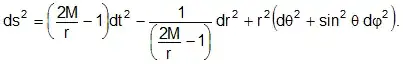
If we transform into the resting coordinate system of an observer inside a black hole, the timelike geodesics will be along the radial dimension of the black hole. Would an observer inside the event horizon of a spherically symmetric black hole observer the radial dimension of the black hole as time? If yes, is it safe to assume that the laws of thermodynamics would hold inside the black hole, in which case the singularity of the black hole would as a zero entropy state be in the past along the radial "time" axis and the high entropy event horizon would be in the future along the same?
What would the cosmology of a spherically symmetric black hole look like from the perspective of an observer inside the black hole. It seems to me that from the perspective of an observer within the event horizon of the black hole:
- The observable universe originates from a singularity (black hole singularity)
- The observable universe expands along the radial (time) dimension
- The exterior of the black hole is not observable from within the black hole
- There would be future boundary conditions defining the faith of the interior (event horizon)
- The interior in other than radial dimension would be relatively uniform for a static black hole
How does time behave inside a black hole from the perspective of an observer inside the black hole? Could such an observer see the interior of the black hole as a universe relatively similar to ours (assuming the arrow of time would be along the radial axis of the black hole).