When objects fall along geodesic paths of curved space-time, why is there no force acting on them?

Question

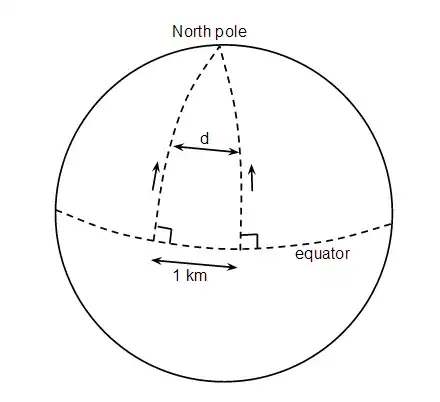
On cseligman.com, it is written that

So, we see things falling with an acceleration which we call the acceleration of gravity,and thinking that we live in a straight line , uniformly moving or stationary inertial frame, we attribute that acceleration to a force, the force of gravity. Whereas in reality,objects falling towards the Earth are moving along geodesic paths with no acceleration and according to modified version of law of inertia, have no force acting on them. They fall simply because the curved space-time near the Earth ...

Now, why do the objects falling towards the Earth move along the geodesic paths with no acceleration? That means the objects don't have any force acting on them, but why? A body in a free-fall moves with acceleration $g$, so, why is it written like that? Why does the author use Law of inertia on freely falling body?? Law of Inertia can only be applied when no external force acts on the body. So, is the freely-falling body accelerates under force of gravity or moves uniformly while moving through geodesic paths as quoted by the author?

Answer 1

Suppose you and I start on the equator, a kilometre apart, and we both head exactly due North in a straight line, so we head off in exactly parallel directions:

Now we know that in Euclidean geometry parallel lines remain the same distance apart. But if you and I measure the distance, $d$, between us we find that $d$ starts off at 1km but decreases as we head North and we eventually meet at the North Pole.

Se we have a paradox: we started out parallel but we moved together. The only explanation is that there is some force pulling us together. But we know there is no force really, it's just that we are moving on a curved surface.

This is what happens in general relativity, though as I'm sure you'd expect it's a lot more complicated (principally because time is curved as well). If you see a freely falling body accelerating towards the earth you'd say there must be a force acting between the body and the Earth, and you'd call that force gravity. But the general relativist would say the Earth and the object are both moving along geodesics, i.e. in a straight line, and it's just that because spacetime is curved the two straight lines converge just as we saw for motion on a sphere. There isn't really a force acting even though it looks like a force to us. That's why gravity is sometimes described as a fictitious force.

Now, there is an obvious problem with my analogy of moving on a sphere, because you and I could start off stationary. Then we are not moving north so we would not approach each other. This is where things get hard to visualise because in GR we are always moving in time even when we are stationary in space. You need to imagine the north direction as moving forwards in time so it's moving forwards in time that causes the two paths to converge.

Actually there is an accelerating object involved in this, and it's you standing on the Earth's surface. How do you know you're accelerating? Well the Earth is pushing at the soles of your shoes and accelerating you upwards. Where there's a force there's an acceleration, so the conclusion must be that the surface of the Earth is accelerating you outwards while the freely falling object you're watching is not accelerating.

If you're interested, twistor59's answer to What is the weight equation through general relativity? explains how to calculate this acceleration, though you may find the maths involved a bit hard going.

Answer 2

Now, why do the objects falling towards the Earth move along the geodesic paths with no acceleration? A body in a free-fall moves with acceleration g, so, why is it written like that?

To understand the passage, we must make two crucial observations.

(1) To person at rest on the Earth's surface, a free-falling object is accelerating towards the center of the Earth, i.e., the distance between the object and surface of the Earth is decreasing at an ever increasing rate.

(2) An accelerometer on the free-falling object reads zero while an accelerometer on the person at rest on the Earth's surface, the accelerometer reads $9.81\mathrm{m/s^2}$.

Clearly, there are two notions of acceleration here. In (1), the object has coordinate acceleration while the person does not. However, in (2), the person has proper acceleration while the object does not.

This is what isn't made clear in the passage. When the author writes

objects falling towards the Earth are moving along geodesic paths with no acceleration

"acceleration" refers to proper acceleration

objects falling towards the Earth are moving along geodesic paths with no proper acceleration, i.e., an accelerometer on the object reads zero

Put less precisely, a free-falling object has no weight. This is why the astronauts on the ISS feel weightless; they, along with the ISS, are in free-fall.

In contrast, a person on the surface of the Earth is prevented from falling towards the center and so is not in free-fall. Thus, the person is on an accelerated world line (path through spacetime) which is why the person feels weight and the attached accelerometer gives a non-zero reading.

For further reading, see for example "The happiest thought of my life"