Why do spin-$\frac{1}{2}$ nuclei have zero electric quadrupole moment?

Question

Why do spin-$\frac{1}{2}$ nuclei have zero electric quadrupole moment? How does this come about, and how can one tell in general whether a spin-$j$ nucleus can have a nonzero quadrupole (or higher multipole) moment?

Answer 1

The answer is: The Wigner-Eckart theorem.

In plain old angular momentum coupling (see Clebsch-Gordan coefficients) we learn that if a system consists of a spin-1/2 subsystem and a spin-2 subsystem, then the total system altogether can be spin-5/2 or spin-3/2, no other value. The rules are

1. $|j_1-j_2| \leq j_\mathrm{total} \leq j_1+j_2$
2. $j_1+j_2+j_\mathrm{total}$ is an integer.

Well, the Wigner-Eckart theorem teaches us that similar rules apply involving operators. The electric quadrupole operator $Q$ can be expressed as a rank-2 spherical tensor operator. When it acts on a spin-1/2 system, the resulting spin can only be $\frac{5}{2}$ or $\frac{3}{2}$. So if you're calculating $\langle\frac{1}{2}| Q|\frac{1}{2}\rangle$, you can group it like $\langle \frac{1}{2}| \;\;\; Q |\frac{1}{2}\rangle$. In other words, this is the inner product of a spin-$\frac{1}{2}$ system with $Q|\frac{1}{2}\rangle$ (which is spin $\frac{3}{2}$ or $\frac{5}{2}$). So they're orthogonal; the inner product is zero. $\langle\frac{1}{2}| Q |\frac{1}{2}\rangle=0$.

By similar logic, dipole moments (electric or magnetic) require spin ≥ 1/2, quadrupole moments require spin ≥ 1, octupole moments require spin ≥ 3/2, etc. (Dipole operators are rank 1, quadrupole are rank 2, octupole are rank 3, etc.)

Answer 2

I want to supplement the formal answer by Steve Byrnes above with a simple observation that makes it obvious in practice that a spin 1/2 cannot meaningfully have a quadrupole moment.

To see this, note that the quadrupole interaction enters the Hamiltonian through a term of the form

$V = \vec{I}\cdot \mathbb{Q} \cdot \vec{I}$,

where $\vec{I}$ is the nuclear spin vector and where $\mathbb{Q}$ is the quadrupole tensor. The quadrupole tensor is symmetric, so there is always a basis in which it is diagonal. So without loss of generality, let's just focus on interactions of the form

$V = \mathbb{Q}_{xx} I_x^2 + \mathbb{Q}_{yy} I_y^2 + \mathbb{Q}_{zz} I_z^2$,

where $\mathbb{Q}_{jj}$ is the $j$th diagonal component of the quadrupole tensor. For a spin 1/2, the spin operators are half the Pauli operators, $I_j = \sigma_i/2$. As a consequence, they always square to $1/4$. So

$V = \frac{1}{4}\left(\mathbb{Q}_{xx} + \mathbb{Q}_{yy} + \mathbb{Q}_{zz}\right) = \frac{1}{4}\textrm{Tr}\left(\mathbb{Q}\right)$.

But because the quadrupole tensor is always traceless, this means that $V = 0$ identically. Thus, even if we posited a quadrupole moment for the spin 1/2, it could not enter the Hamiltonian. The algebra of the spin-1/2 operators only allows for zero quadrupole interaction.

Answer 3

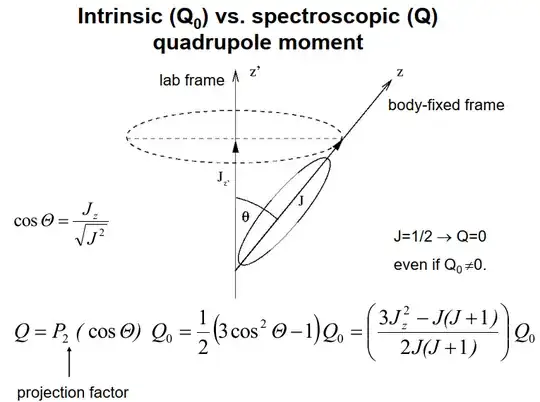
They need to have zero $Q$ spectroscopic quadrupole moment: inserting $J=J_z=1/2$ to below formula from https://slideplayer.com/slide/4813696/ .

However, they can have nonzero $Q_0$ intrinsic electric quadrupole moment, which turns out nonzero for example for proton:

• https://journals.aps.org/prc/abstract/10.1103/PhysRevC.63.015202
• open access preprint ArXiv version at https://doi.org/10.48550/arXiv.hep-ph/0101027