Can somebody please provide a derivation of how to calculate excluded volume of two rods with angle of intersection being $\gamma$. rods are cylinders, capped with semi-spheres. Onsager theory of hard rods is based on this and I cant seem to find a derivation for excluded volume.
Asked
Active
Viewed 1,941 times
1 Answers
2
In order to calculate the excluded volume between two spherocylindric rods, the relative angle between them changes the base area of the excluded volume, usually taken as a parallelogram, and the thickness of rods, i.e. $D$ the height of the excluded volume. Consider the picture below, taken from (Basic Concepts for Simple and Complex Liquids, from Jean-Louis Barrat, Jean-Pierre Hansen)
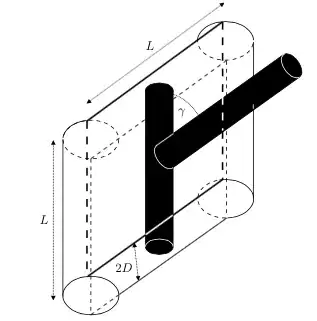
As you can see, we have a base in the form of a parallelogram with area $L^2 \sin\gamma$ and with thickness $2D$, excluded volume: $$V_{ex}=2L^2D|\sin \gamma|.$$
The $2$ comes from the fact that the volume $L^2D|\sin \gamma|$ is excluded for the other rod on both sides.
Ellie
- 4,219
- 2
- 22
- 38