In complex numbers, we define a harmonic function as a twice continuously differentiable function such that the Laplace operator acting on it gives zero. Can anybody explain me the physical interpretation of harmonic functions?
2 Answers
Firstly, I'd like to recommend Tristan Needham's book Visual Complex Analysis which is an excellent text and very accessible to physicists. In his own words (p. 515):
The Laplacian of $\Phi$ at $p$ measures the amount by which the average value of $\Phi$ on an infinitesimal circle centered at $p$ exceeds the value of $\Phi$ at $p$ itself. More precisely, if $r$ is the infinitesimal radius of this circle, then
$$\langle \Phi \rangle - \Phi(p) = \frac{1}{4}r^2 \Delta \Phi$$
Towards a derivation, consider the scalar field $\Phi$, and a gradient vector field $\nabla \Phi$. Physically, one may think of $\Phi$ as a potential, and $\nabla\Phi$ as the lines of force. The flux out of a circle $C$ of radius $r$ is,
$$2\pi r \partial_r \langle \Phi \rangle$$
If $\Phi$ is harmonic, then $V$ is sourceless, and the flux vanishes as a consequence of the definition above of the Laplacian. From this, we see $\langle \Phi \rangle$ is independent of $r$, and it follows that if we shrink $C$ down to the center point $p$, this $r$-independent value must be $\Phi(p)$.
Now suppose the flux is non-zero, but that the flux-density $\Delta \Phi$ is constant. As a consequence of Gauss' divergence theorem, the flux must be of the form, $nr^2 \Delta \Phi$. Inserting into our original flux, we find,
$$\partial_r \langle \Phi \rangle = \frac{1}{2}r\Delta \Phi$$
which you can integrate to find the first definition of the Laplacian. To complete the derivation, as Freedham states, it is 'only necessary to observe that the Laplacian of an arbitrary $\Phi$ is constant within an infinitesimal circle.' Freedham goes on to show how this result can be used to geometrically prove the conformal invariance of the Laplacian. This implies a harmonic function is only harmonic if and only if all conformal transformations maintain its harmonicity.
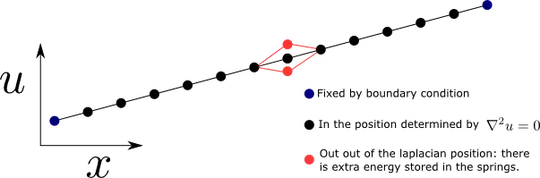
Imagine an elastic fabric streched over a flat frame. If the frame is then bent out of the plane, the shape of the fabric will follow. The equation $ \nabla^2 u = 0 $ can be used to model such, where $u$ represents the displacement of the frabric with respect to the initial configuration.
As explained here the laplacian $\nabla^2 u(x_0)$ is proportial to the average of $u(x)-u(x_0)$ in a small ball around $x_0$. So having $\nabla^2 u = 0$ means that at every point, $u$ would equal to the average of its neighboring points.
With this interpretation, it can be seen why the fabric should satisfy such an equation. If you think about it in 1D as a chain of points that are joined by springs, the configuration with minimal energy is where each point is in between its neighbours.