Is $E^2=(mc^2)^2+(pc)^2$ or is $E=mc^2$ the correct one?

Question

I have been having trouble distinguishing these two equations and figuring out which one is correct. I have watched a video that says that $E^2=(mc^2)^2+(pc)^2$ is correct, but I do not know why. It says that $E=mc^2$ is the equation for objects that are not moving and that $E^2=(mc^2)^2+(pc)^2$ is for objects that are moving.

Answer 1

Let me clarify some confusions in the notation that other answers have alluded to but not clearly mentioned.

Historically, physicists liked to talk about two different definitions of mass

• The first is the rest mass of a particle $m_0$. This is the mass of the particle when it is at rest. For example, the rest mass of the electron is $(m_0)_{electron} = 9.1 \times 10^{-31}~Kg$. This is an absolute constant that is independent of the speed of the particle.

• The second is the relativistic mass $m$. This is the apparent mass of the particle when it is moving with speed $v$. It is related to the rest mass via the relation $$ m = \gamma m_0 = \frac{m_0}{\sqrt{1-v^2/c^2}} $$ Note that the relativistic mass is NOT a constant. It depends on $v$.

In this historical notation, Einstein's famous formula that is completely correct in all frames is $$ E = m c^2 $$ However, it turns out via a series of algebraic manipulations that this equation also implies $$ E^2 = ( m_0 c^2)^2 + (pc)^2 $$ Let us prove this. $p$ is the momentum of the particle defined by $p = m v = \gamma m_0 v$. Thus $$ (m_0 c^2)^2 + (pc)^2 = m_0^2 c^4 + \gamma^2 m_0^2 v^2 c^2 = m_0^2 c^4 \left( 1 + \frac{\gamma^2 v^2}{c^2} \right) $$ Now, we have the property $$ 1 + \frac{\gamma^2 v^2}{c^2} = 1 + \frac{\frac{v^2}{c^2}}{\left( 1 - \frac{v^2}{c^2} \right) } = \frac{1}{ \left( 1 - \frac{v^2}{c^2} \right) } = \gamma^2 $$ Thus $$ (m_0 c^2)^2 + (pc)^2 = m_0^2 c^4 \gamma^2 = (\gamma m_0)^2 c^4 = m^2 c^4 = (mc^2)^2 = E^2 $$ Thus, in summary, in the historical notation, we have two completely equivalent formulae $$ \boxed{ E^2 = (m c^2 )^2 = (m_0 c^2)^2 + (pc)^2} $$

In modern day notation, physicists have decided to drop discussion of the relativistic mass $m$ since it is not an absolute constant and depends on the speed of the particle. Nowadays, we only talk about the rest mass, $m_0$. However, in a confusing notational change physicists today decided to use $m$ for the rest mass (which in today's notation is not confusing at all, since we don't talk about relativistic mass, but it is often confusing to students who try to compare Einstein's original papers with books written today).

Following modern day notation then, we only have ONE equation, namely $$ \boxed{ E^2 = (m c^2)^2 + (pc)^2 } $$ where in the above equation $m$ is now the rest mass.

Answer 2

Both are correct, within the domains for which they are correct.

More seriously, the general relation

$$ E^2 = m^2c^4 + p^2c^2$$

holds for all objects, whether they have mass or not, whether they are moving or not.

The special case $E = mc^2$ is for $p = 0$, i.e. objects which do not move, as you said.

The special case $E = pc$ is for objects which have no mass, i.e., photons.

Answer 3

I agree with answer of ACuriousMind, but I think it might also help to think about it like this....

$E^2=m_0^2c^4+p^2c^2 =m^2c^4$

where $m_0$ is the rest mass and $m$ is the relativistic mass (or inertial mass), defined as $m = \gamma m_0 = m_0 / \sqrt{1 - v^2/c^2}$.

The relatavistic mass increases as the momentum of the mass increases. At rest the two are equal to each other. As the speed of an object and its momentum increase the mass of the object increases.

so I think about it as

$E^2=m_0^2c^4+p^2c^2$

and

$E=mc^2$

Answer 4

The equation $$E^2=(mc^2)^2+(pc)^2$$ represents the correct energy-momentum relationship. It gives the total energy $E$ for an object of invariant mass (rest mass) $m$ that is observed to move with momentum $p$. This equation is applicable regardless whether the object is observed to be in motion ($p \ne 0$), or is observed to be at rest ($p = 0$). In the latter case, the energy-momentum equation simplifies into the well-known $E=mc^2$.

As an aside (some might call it nitpicking), when discussing the generics of the energy-momentum equation, it is good form to write the equation such that both sides of the equation are independent of the frame of observation chosen: $$ E^2 - (pc)^2 = (mc^2)^2$$ Same math, different physics. (Note that this relativistically invariant relationship is simply the expression for the square norm of the energy-momentum four-vector.)

Answer 5

The best way to clarify the issue is to just recap what Einstein, himself, originally wrote on the matter in his $E = m c²$ Paper (English translation).

He uses $V$ for light speed $c$. I'll use $c$ and $α$ for $1/c^2$, that is: for his $1/V^2$. The paper has to be taken in the context of his 1905 Special Relativity paper (English translation), where he derived the equation $$K = mc^2 \left(\frac1{\sqrt{1 - α v^2}} - 1\right)$$ for a body's kinetic energy, $K$, for a body of rest-mass $m$ moving at a speed $v$. (He called it $W$, instead of $K$, in that paper.) It can be rewritten, with a little algebra, as $$K = \frac{Mv^2}{1 + \sqrt{1 - α v^2}}\quad\left(M = \frac{m}{\sqrt{1 - α v^2}}\right)$$ where $M$ is the body's "moving mass". The connection with Newtonian physics becomes much more clear, this way, since setting $α = 0$, gives $M = m$ and $K = ½M v^2 = ½m v^2$. Newtonian physics is (mostly) recovered from Special Relativity by taking the limit $α → 0$.

In his $E = mc^2$ paper, he uses $E$ for a body's energy at rest (its internal energy), $K$ for the body's kinetic energy and $H$ for the body's total energy. Then $$H = E + K.$$

He devises a situation where the body at rest is emitting a quantity of light of energy $L$ with $½L$ of it going one way and $½L$ of it going the other way, so that the recoils balance out and the body remains at rest. He uses $(⋯)_0$ to refer to the before-situation, the body's rest-frame, and $(⋯)_1$ to refer to the after-situation.

In the body's rest-frame, he gets $$E_0 = E_1 + L,$$ for the internal energy by energy conservation. In a moving frame that is moving at a speed $v$ with respect to the body, he notes that the energy of the light emitted is seen as $L/\sqrt{1 - α v^2}$, based on his Special Relativity paper. Therefore, $$H_0 = H_1 + \frac{L}{\sqrt{1 - α v^2}}.$$

Subtracting out $K = H - E$, he gets before-versus-after relation for kinetic energy of $$K_0 = K_1 + L \left(\frac1{\sqrt{1 - α v^2}} - 1\right).$$ That means that rest mass, $m$, itself, must suffer a before-versus-after change, with $$K_0 = m_0 c^2 \left(\frac1{\sqrt{1 - α v^2}} - 1\right),\quad K_1 = m_1 c^2 \left(\frac1{\sqrt{1 - α v^2}} - 1\right)\quad⇒\quad m_0 c^2 - m_1 c^2 = L.$$

Therefore, the mass difference, before versus after, dividing out by $c^2$ (and using my $α = 1/c^2$) is: $m_0 - m_1 = α L$. For Newtonian physics, $α = 0$, so $m_0 - m_1 = 0$. So, this makes a clear contrast between Newtonian physics versus Special Relativity.

That's the recap of the paper.

---

In fact, take a closer look. The moving mass $M$ is just the rest mass $m$ plus the mass equivalent of the kinetic energy, itself: $M = m + α K$, so the energy-mass relation is already tacit. Check the algebra!

So, if you let $$w = \frac{v^2}{1 + \sqrt{1 - α v^2}}$$ stand for the multiplier that becomes the $½ v^2$ of the Newtonian expression for kinetic energy ($K = ½ m v^2$) when $α → 0$, then you can explain the moving mass $M$, itself, as the rest mass, $m$, plus the mass equivalent $α m w$ of its kinetic energy $m w$, plus the mass equivalent $α (α m w) w$ of the extra mass' kinetic energy $(α m w) w$, plus the mass equivalent $α (α (α m w) w) w$ of that extra mass' kinetic energy $(α (α m w) w) w$, and so on. In total, you get the sum $$M = m + α m w + α (α m w) w + α (α (α m w) w) w + ⋯ = m (1 + (α w) + (α w)^2 + (α w)^3 + ⋯).$$ The series $1 + x + x^2 + x^3 + ⋯$ adds up to $1/(1 - x)$, if $|x| < 1$. It is always the case that $|α w| < 1$, for sub-light speeds $|v| < c$. So, $$M = \frac{m}{1 - α w} = \frac{m}{\sqrt{1 - α v^2}}.$$ Check the algebra: $1 - αw = \sqrt{1 - α v^2}$!

Correspondingly, the body's momentum, $p$, has to include all of the mass, so that it is $p = M v$ in Special Relativity, instead of the $p = m v$ of Newtonian physics. Actually, it's still $p = M v$ even in Newtonian physics, but $M = m$, in that case.

In your terms $E = m c^2$ is for the internal energy and rest mass, while $H = M c^2$ is for the total energy and moving mass, with $$E = m c^2,\quad H^2 = \left(m c^2\right)^2 + (p c)^2.$$

This is the answer you were looking for.

But bear in mind (and it's time for a little excursion) ...

---

Einstein never actually made either of these inferences! Nor did he assert either of those equations in his paper. All that he said was that $Δm = m_0 - m_1 = -αL$. To make the contemporary statement $E = m c^2$, i.e. that $m = α E$, requires also the assumption that the rest mass $m$ is all accounted for by the internal energy $E$! That's a separate, and additional, assumption.

I don't know who made the extra assumption, or when, but I think it was Einstein who did, some time later in the 1905-1910 period, probably after Minkowski's 1908 paper. In his 1905 $E = mc^2$ paper, Einstein actually did keep an extra additive constant $C$ around, but put it in with $K$, by writing $H - E = K + C$. You could just as well absorb $C$ into a redefinition of $E$, which puts the spotlight back onto it.

In general, the only inference you can make from his analysis is that $m = μ + α E$ for some "intrinsic" mass $μ$. The extra assumption amounts to the assertion that $μ = 0$.

In more contemporary language, making that assumption would reduce the symmetry group for Special Relativity from Poincaré × ℝ to Poincaré. The extra degree of freedom associated with $μ$, and associated with keeping $E$ independent of $m$, would be lost. There are lots of places where you want that to remain intact: like in Quantum Field Theory. (For instance, you could generalize the Wightman axioms to include an independent internal energy and Poincaré × ℝ representations, the result being that you now have a slot for zero-point energy.)

However, in equally-contemporary language, the assumption $μ = 0$ breaks the Correspondence Principle with non-relativistic physics. This was a case of people being in the wrong place at the wrong time. During the early 20th century, when the groundwork for Special Relativity had been laid out, the symmetry group for non-relativistic theory was understood to be the Galilei group, which has only 10 generators, like the Poincaré group, not 11 like Poincaré × ℝ. However, by the middle of the 20th century, it eventually came to be realized that the correct symmetry group for non-relativistic physics is not the Galilei group, but its central extension: the Bargmann group, which has 11 generators.

That alteration also amends what should be taken to be the Correspondence Principle and that, too, had to be accounted for. However, it was never properly accounted for, notwithstanding Wigner and İnönü.

Poincaré is not what has an $α → 0$ limit to Bargmann. Rather, it's Poincaré × ℝ that does. So, if you want to respect the Correspondence Principle - as it would be understood today - then you should actually retain "internal energy" as an independent quantity, rather than one that's tied directly to rest mass, and keep $μ$ around.

That would be to generalize the contemporary formulae $M = α H$ and $m = α E$ (i.e. $H = M c^2$ and $E = m c^2$) to $M = μ + α H$ and $m = μ + α E$, while $M - m = α (H - E) = α K$ (i.e. $K = (M - m) c^2 = M w$) continues to hold. Because Einstein's paper only made assertions about the energy difference $K = H - E$, any extra additive contribution $μ$ to $H$ and $E$ would remain unspoken for.

The formula $$H = M w + m c^2 = m c^2 \left(\frac1{\sqrt{1 - α v^2}} - 1\right) + m c^2 = \frac{m c^2}{\sqrt{1 - α v^2}}$$ would be generalized to and replaced by $$H = M w + E = m c^2 \left(\frac1{\sqrt{1 - α v^2}} - 1\right) + E = \frac{m}{\sqrt{1 - α v^2}} \frac{v^2}{1 + \sqrt{1 - α v^2}} + E.$$

The non-relativistic limit of this, as $α → 0$ would be $H = ½ m v^2 + E$, which is actually the more correct formula for the energy of a body in Newtonian physics, since it is additive. In non-relativistic theory, the total energy $H$ of two bodies with respective data $\left(m_0, v_0, E_0, H_0\right)$ and $\left(m_1, v_1, E_1, H_1\right)$, can be made additive $H = H_0 + H_1$, by taking $$m = m_0 + m_1,\quad v = \frac{m_0 v_0 + m_1 v_1}{m_0 + m_1},\\ E = E_0 + E_1 + δE\quad \left(δE = \frac{m_0 m_1}{m_0 + m_1} \frac{|v_0 - v_1|^2}2\right).$$ The internal energy of a body includes the kinetic energy that arises from the jostling about of a body's components ... plus the internal energy of the components, themselves. Binding energy is also included in there, as well.

If you keep $m$ and $E$ independent, then you can continue to treat both the total energy $H$ and the moving mass $M$ as additive, and independently so, by making $μ$ additive, so that $H = H_0 + H_1$, $M = M_0 + M_1$ and $μ = μ_0 + μ_1$.

In Special Relativity, there is a similar compensatory expression for the sum $E = E_0 + E_1 + δE$ - but one that also applies to the rest mass $m = m_0 + m_1 + α δE$. That continues to be the case, but in place of $E = m c^2$, you'd have $E = (m - μ) c^2$.

The body's total energy would then be $$H = (M - μ) c^2 = (M - m) c^2 + (m - μ) c^2 = K + E.$$

In the non-relativistic limit as $α → 0$, $μ → m$. However, $μ$ shares the additivity property of the non-relativistic $m$, unlike $m$ in Relativity.

The extra assumption that Special Relativity makes, that reduces the symmetry group from Poincaré × ℝ to Poincaré is that $μ = 0$. However, $μ$ is the very thing that distinguishes the Galilei group from the Bargmann group! (It's called the "central charge" and is the 11th generator). So, the Correspondence Principle is broken.

It also breaks the Correspondence Principle since forcing $μ = 0$ means that $H$ means no longer has a meaningful non-relativistic limit for bodies with non-zero rest mass $m$, because the formula would become $H = K + m c^2$ and the $m c^2$ part of $H$ would blow up to infinity.

In fact, if you set $μ = 0$, then in the limit $α → 0$ you only get the mass $m = 0$ representations of the Galilei group - which was the big problem that Wigner and İnönü worked on trying to get around. However, their solution was cumbersome because it, too, was a case of people being in the wrong place at the wrong time. It mostly predated the idea of the Bargmann group, and came from a time when only the concept of its precursor was around: the "projective representations" of the Galilei group.

Answer 6

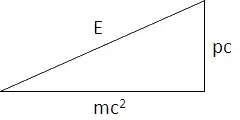
All of the other answers are great, and I highly recommend reading them. However, I think something is missing if you don't attempt to get an intuitive understanding with geometry:

This triangle shows that the equation $E^2=(mc^2)^2+(pc)^2$ can be represented via a sort of reverse Pythagorean theorem. The special case of $E=mc^2$ can be found by setting $p$ to zero, and appears as if the $pc$ side of the triangle is zero in size, changing the shape to a line with $E$ on top and $mc^2$ on the bottom. Likewise, for light, we can show the special case of $E=pc$ by setting the rest mass $m$ to zero, which transforms the triangle into a vertical line with $E$ on the left and $pc$ on the right.

Answer 7

Much of this is hard-won insights after a couple of decades of independent study. Look into it, and I think you might find there's something pretty useful here.

Newton's Second Law can be written:

$$\frac{\text{Impulse}}{\text{mass}} = \text{Change in Velocity}.$$

But in relativistic mechanics we have

• Impulse/mass (in ls/s) = $\sinh(w)$,
• Change in Velocity (in ls/s) = $\tanh(w)$
• Time Dilation/Length Contraction Factor (in s/s or ls/ls) = $\cosh(w)$

where $w$ is the rapidity. When rapidity is small, $\sinh(w)= \tanh(w) = w$

You can see part of this in $$E^2 = p^2 c^2 + (mc^2)^2$$

So this equation is essentially the hyperbolic trig equivalent of Pythagoras theorem.

$$(mc^2)^2 \cosh^2(w) = (mc^2)^2\sinh^2(w) + (mc^2)^2 $$

or

$$(mc^2)^2 \gamma^2 = (mc^2)^2 \left(\frac{\text {impulse}}{\text{mass}} \text{(in ls/s)}\right)^2 + (mc^2)^2 $$

You can also get the kinetic energy out of this equation by subtracting 1 from the time-dilation factor, and multiplying the result by $mc^2$. The equation is not terribly useful for that purpose at low velocities, though, since the time-dilation factor, $\gamma$, will be something like 1.00000000004 and it won't fit into your calculator.

Once you confirm that all this is really hyperbolic trig, if you can find a calculator with easy access to hyperbolic trig functions, you'll find it much easier to put things into rapidities.