A force is exerted on a body, kinetic energy increases but no work is done by the force. Why?

Question

After reading the article, I was totally perplexed . I was reading the External forces and internal energy transfers in Principles of Physics by Resnick,Halliday,Walker. It goes like that

An external force can change the kinetic energy or potential energy of an object without doing work on the object- that is, without transferring energy to the object. Instead,the force is responsible for transfers of energy from one type to another inside the object.

Then they cited an example.

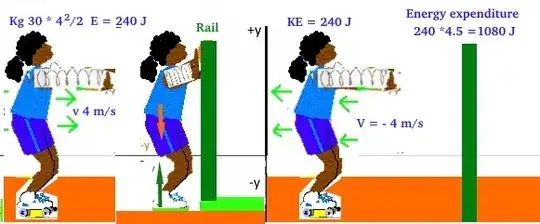
An initially ice-skater pushes away from a railing and then slides over the ice. Her kinetic energy increases because of an external force $\vec{F}$ on her from the rail . However, that force does not transfer energy from the rail to her. Thus,the force does no work on her.

What is going on here? First they said the KE increased due to that external force. Then they said the force did no work. If force were given and displacement had not occured then I would say yes! the work done would be 0 inspite of force being applied.

But here, displacement occured and according to the book , the kinetic energy increased due to the force but due to some cause the force did no work! Is it magic??

I am really confused. Please help me giving a strong explanation to this.

Answer 1

I agree with CuriousOne that the example is more confusing than helpful, but this is the way I would explain it.

Suppose you take a spring, place it on the ground then compress it. If you now suddenly let go of the spring it will rebound and bounce upwards off the ground:

The spring clearly has work done on it because its kinetic energy increases and that increase must have come from somewhere. However the ground can't have done any work on the spring because the ground hasn't moved. It should be obvious that the potential energy in the compressed spring has been converted into kinetic energy of the uncompressed spring - in effect the spring has done work on itself. This is what your book means by:

transfers of energy from one type to another inside the object

i.e. potential energy of the compressed spring has been converted into kinetic energy of the uncompressed spring.

In the case of the skater the skater's arms correspond to the spring and the rail corresponds to the ground. The skater's arm isn't a spring, of course, because it's chemical energy not potential energy being converted to kinetic energy by the skater's muscles. Nevertheless the same principle applies.

Answer 2

I think this is a good example, and should be studied and understood carefully. But I don't know where the book goes after making it. Whether or not it is poorly stated depends on the surrounding context.

It focuses attention on two things:

1.) the skater is a deformable body. The center of mass is not fixed in the body.

2.) work is defined as a force times the displacement of the point of application.

(And, arguably a third aspect: the skater carries a store of chemical energy. But this fact is aside the point being made.)

In this case, the point of application does not move. There is no external work from that force. Both of these points are important to understand and remember. Typically, up to this point in a course, problems are implicitly formulated in terms of a point-particle model of an object. No internal structure. When deformable bodies are considered, certain things that work for point-particles no longer work. Additional analysis is needed.

Note that there is internal work being done. Chemical reactions contract muscle fibers. The fibers apply forces to tendons. Now there is a force and a displacement of the application of the force.

Answer 3

An initially ice-skater pushes away from a railing and then slides over the ice. Her kinetic energy increases because of an external force F⃗ on her from the rail . However, that force does not transfer energy from the rail to her. Thus, the force does no work on her.

This is simply confused: This example is nothing but an elastic collision between the girl and the rail. The example given by John is appropriate but I do not agree with him that the arms behave differently from a spring. Of course the ultimate source of energy is chemical, but the girl as a system behaves exactly like a steel spring or a football hitting the rail.

If the skater (m = 30 Kg) had a spring and was travelling at v = 4 m/s she would have KE = 240 J and would bounce back at (roughly) the same speed. If she stretches her arms and pushes at the rail (like a spring) she can acquire the same speed of 4 m/s producing net work of 240 J. Because of human muscle inefficiency she'll have to burn 4-5 times that amount of calories $\approx 1080 J$

The body is compressed against the rail like an elastic ball, then it stretches back (in a ball the whole body, in a skater the arms, in a swimmer in a pool or in a high-jumper the legs) giving acceleration to the whole body. In the case of a xollision the compression is given by the initial v and KE, in the case of the push by the girl, by the calories burned in the muscles. The rail transfers no energy just exert a (passive) reaction to the action of the skater (it might budge a little), as per third law. The energy does not increase because of an external force acts on her.

Answer 4

At this point, we simply need to remember Newton's 1st law. For every force, there is an equal and opposite force. First off, make no mistake, the railing did provide a force for her. The railing pushed her at exactly the same amount that she pushed it. However, since it is cemented into the ground, the force was not enough to move it whatsoever. Work is contingent on two factors; Force, $F$, and Distance $d$: $$ W=Fd \\ W=F*0 \\ W=0 $$ The Force applied is completely irrelevant if the railing does not move. She performed no work on the railing, nor did the railing provide work on the skater. If there is no distance over which the Force is moving, no work is done.

The reason Kinetic Energy increases is because of the nature of the formula: $$ KE = \frac{mv^2}{2} $$ And: $$\Sigma F=ma$$ Kinetic Energy is not solely contingent upon Work energy. A force is still applied, just not over a distance.

Answer 5

I agree with garyp, this is an important case but I think there is an important fact which has not been noticed in the book nor in the above answers:

In this example (skater, also the example of the car which moves due to the static friction) the external force does not do work and this has an important physical meaning that is, no energy is being transferred from outside into the system (person or car).

Therefore this is a case for which the work-energy theorem ($W_{external}=\Delta K$) doesn't apply. In other words, kinetic energy has changed but external work is zero. So we should reformulate the work-energy theorem in order to include systems with internal structure. That is why in the book another term is introduced in the right-hand side of the energy equation: $W=\Delta K+\Delta U+ \Delta E_{th}+\Delta E_{int}$. The last term has not any work associated with it. Therefore this last equation is the law of conservation of energy rather than the work-energy theorem.

Answer 6

Apply the work energy theorem. viz. $\Delta K +\Delta V = \Delta W$ where $\Delta K = K_f - K_i$ etc. Now we have $\Delta W = 0 ,~V_f = 0,~ V_i >0,~ K_i = 0$. Hence it follows that $K_f = V_i (>0).$