3

Suppose you are in space (or on a frictionless surface) next to another object of the same mass $m$ as you. Take the reference frame of the center of mass of you and the object (so there is zero velocity initially). Now suppose you push on the object with a constant force $F$ for some time $\Delta t$ to "jump off" the object.

During the time $\Delta t$, there is an acceleration $a = F/m$ for both you and the object in opposite directions. The final velocities of you and the object are $v = a\Delta t$.

The object has final kinetic energy $KE = \frac{1}{2}ma^{2}\Delta t^{2}$ and you have final kinetic energy $KE = \frac{1}{2}ma^{2}\Delta t^{2}$. Together, there is total kinetic energy $$ KE = ma^{2}\Delta t^{2}. $$

The work done by you on the object is $W = F\cdot \frac{1}{2}a\Delta t^{2} = \frac{1}{2}ma^{2}\Delta t^{2}$, so this is how much potential/chemical energy you've transferred from yourself to the other object in the form of kinetic energy.

Now the issue is, this only accounts for half of the total kinetic energy. There is also work done by the object on you, but the issue is, that other object didn't have any potential energy. So how can the other object do work on you, without transferring any energy to you? What is the right way to think about this situation?

Qmechanic
  • 220,844
MaximusIdeal
  • 8,868

4 Answers4

4

There is also work done by the object on you, but the issue is, that other object didn't have any potential energy. So how can the other object do work on you, without transferring any energy to you?

In this problem energy transfers only from you to the object.

Consider, as a model, that the object is a rigid block and you are a block attached to a compressed spring. Now, as you are pushing the object to the right, the point of contact moves to the right. So the force on the object has a positive power $P=\vec F \cdot \vec v$, while the force acting on you has a negative power $-P=-\vec F \cdot \vec v$. So power goes into the block and power goes out of you.

Now, in the process of pushing the spring is extending twice as fast as the block is moving. So you are losing elastic energy twice as fast as you are transferring mechanical energy, so half of the elastic energy you lose stays with you and does not go out. But this energy is no longer elastic, it is now kinetic energy.

So the blocks increased KE is due to you doing work on it. Your increased KE is not due to any work (which is a transfer of energy). Instead it is an internal change of energy from elastic to kinetic.

The force from the block on you increases your momentum, but does not increase your energy.

Dale
  • 117,350
4

Often one has to be careful including the forces applied, work done by etc, by the human body so I will first include you as an inanimate object.

System - you, object and a device which I will elaborate on later.
The device exerts a constant magnitude force on you and the object but in opposite directions.

The free body diagrams are shown below with the magnitudes of all the forces being the same, $F$.

enter image description here

Suppose the separation between you and the object increase by $d$, ie you move $d/2$ and the object moves $d/2$ to the right with the device not moving at all.

The device does work $F_{\rm yd}\cdot d/2$ on you and the device does work $F_{\rm od}\cdot d/2$ and no work is done on the device because it does not move.

Doing the sums it can be shown that the total work done by the device, $Fd/2+Fd/2=Fd$ is equal to the kinetic energy gained by you and the object $2\times \frac 12 m v_{\rm final}$ where $v_{\rm final}$ is the final speed of both you and the object after separation with energy being conserved.

Now what is this device?
It could be some sort of spring arrangement with stored elastic potential energy or it could be a cylinder which has massless and frictionless pistons at each end with a chemical reaction (explosion) going on inside the cylinder.

However in this case it the parts of you body, the muscles, which allow you to move using up chemical energy.
The process of what actually happens is very complex as your body can no longer be assumed to be rigid and the forces are being generated by the contraction of your muscles.
Note that if it is your hand that does the pushing, the hand in contact with the object will have to be moving at the same velocity as the object.

Although what happens between the initial and final state is so complex that I have not attempted to describe it in any detail, I hope that I have shown you that it is you who has to do all of the work.

Farcher
  • 104,498
2

I think it is worthwhile here to first make sure that assigning the qualifications 'positive work' and 'negative work' is done in a guaranteed consistent way.

Simplest instance: in celestial mechanics: a small object orbiting a far heavier primary. I will refer to the two objects as 'primary' and 'secondary'.

Let the secondary be in an eccentric orbit. Example: the orbit of Halley's comet. When Halley's comet is on its way to its point of closest approach (to the Sun) the Sun's gravity is doing positive work, increasing the velocity of Halley's comet. The comet goes along its point of closest approach, and from there starts climbing again. During the climbing phase the Sun's gravity is doing negative work on Halley's comet.

There are two aspects to get right.
There is the sign of some particular work done, and there is the issue of attribution: which object is doing that work.


Next we move to a case that is one degree less simple:

Let there be two celestial bodies, of equal mass, orbiting each other, in eccentric orbit.

The two celestial bodies are continuously doing work upon each other. During the contracting phase of the orbit each is doing positive work upon the other celestial body, increasing the velocity of the other celestial body. Conversely, when the two celestial bodies are swinging away from each other again both are doing negative work upon the other celestial body.


Next example: the case described in the answer by Farcher: two objects of equal mass, and a device that that acts like a gas spring. When the piston of the gas spring is pushed into the cilinder the gas spring converts the work done to potential energy.

During compression of the gas spring: the work done by the gas pressure is negative work. When the gas spring expands again the gas pressure is doing positive work.


We set up a collision of the two objects, in such a way that the kinetic energy of the objects converts to potential energy stored in the gas spring, and then the gas spring pushes the two objects apart again.

Now, returning to the case of gravitational interaction for a moment: we could choose to describe that interaction in terms of storing gravitational potential energy, but that is unpractical. The practical choice is to treat the case as a direct object-to-object force. Do that consistently, and no self-contradiction will arise.


Now the case where the gas spring is acting as a repulsive force between the two objects.

We have the option of treating that repulsion as a generic repulsion, and think of the case as two objects, exerting a repulsive force directly upon each other. As long as we consistently treat the case in terms of exerting a force directly upon each other no self-contradiction will arise.

The other option is to treat the gas spring explicitly as a participating factor. Then there is no longer such a thing as object A doing work upon object B. All tracking of force and doing work must be expressed in terms of a pair of participating factors. When you treat the gas spring explicitly as a participating factor then you have two pairs: object A and the gas spring, and object B and the gas spring.



Let two objects be initially adjacent. You have a gas spring that can be locked in compressed state, ready to be released with a trigger

You compress the gas spring, and you position the gas spring in between the two objects. Upon releasing the gas spring: the gas spring is doing work on both of the objects, accelerating them away from each other.



Summerizing:
Treated as two objects exerting a repulsive force directly upon each other: as the objects accelerate away from each other each object is doing positive work upon the other object.

Treated with explicit participation of the entity that interconverts kinetic and potential energy: work done by the objects is work done upon that energy interconverting entity. Work done by the energy interconverting entity is done upon the objects.

Cleonis
  • 24,617
1

I finally understand how to think about my question in a way that I can put into my own words. I will address the last part of my OP, which said,

There is also work done by the object on you, but the issue is, that other object didn't have any potential energy. So how can the other object do work on you, without transferring any energy to you? What is the right way to think about this situation?

The issue stemmed from confusing how work is treated in an intro mechanics course vs how work is treated in a thermodynamics course. See the linked posts at the end of this post. Also, we should point out that for extended bodies there is a difference between body forces and contact forces. I will focus only on contact forces in this discussion (so no gravity or electromagnetism).

Work

As pointed out in this post and this post, there is a difference between "work due to a particular force" and the "center of mass work"/"net work"/"pseudowork."

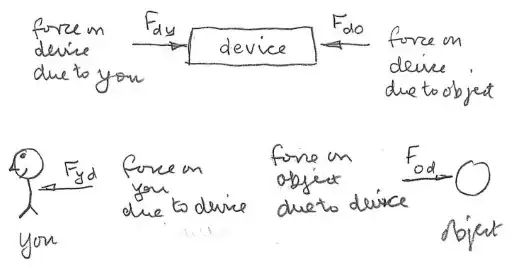
When you are dealing with work due to a particular contact force $F$ on a body/system, you must always track the position at which the force is applied when calculating $dW_{F} = F\, dx$. This is how work is calculated in thermodynamics, and if $F$ is the force done by an outside system or environment on the system you are interested in, then $W_{F}$ is the energy transfer into the system due to the force $F$.

Summing all such work gives you the energy transfer into the system due to all the contact forces acting on the system. When we add energy transfer due to heat, if any exists, we obtain the equation for the first law of thermodynamics.

Now there is another form of work, commonly called net work, which is invoked in the study of Newtonian mechanics. It is known that when you sum all forces $F_{i}$ acting on a body/system, the center of mass obeys $\sum_{i} F_{i} = MA$ ($M$ being total mass and $A$ being the acceleration of the center of mass) even if the forces are not applied at the center of mass. Now the work-energy theorem then states that if we define $dW_{\text{net}} = F_{\text{net}}\, dX$ (where $F_{\text{net}} = \sum_{i} F_{i}$ and $X$ is the center of mass position), then the change in the translational kinetic energy associated with the motion of the center of mass is $\Delta KE = W_{\text{net}}$. Note this theorem, as I stated it, discounts kinetic energy associated with internal motion and it discounts any mention of potential energy.

Remarkably, the two forms of work I pointed out are different, and you don't run into any contradiction if you track all forces carefully enough.

Original Scenario

Now how does all this apply to the original question? Going back to the original scenario, let us take system $1$ ($S_{1}$ for short) to be the person jumping off and let us take system $2$ ($S_{2}$ for short) to be the other object.

Alternatively, we can imagine that we have two blocks with a spring in the middle (the specifics of what mechanism is used to push objects apart or the force law is not important), and we can take $S_{1}$ to be the system consisting of one block plus the spring attached to it and $S_{2}$ to be the system consisting of the other block. Note that in the analysis, we will not need to consider the spring as its own system! Other posts that say the spring or whatever pushes things apart has to be its own system are misleading!

Choose a coordinate system so that (the center of mass of) $S_{1}$ moves in the $+$ direction along some axis and (the center of mass of) $S_{2}$ moves in the $-$ direction along the same axis when the two are pushed apart.

Assume $S_{1}$ and $S_{2}$ are pushed apart and end up with final velocities $v_{f}$ and $-v_{f}$ along some axis. When $S_{1}$ and $S_{2}$ are pushed apart, the potential/chemical energy of $S_{1}$ is converted to the kinetic energies of $S_{1}$ and $S_{2}$.

When the two systems are being pushed apart, the following two things are true:

  1. Since $S_{1}$ is expanding (either because the person is jumping off in one scenario or the spring is expanding in the other scenario), the contact point is moving in the direction of $S_{2}$ with overall velocity.
  2. The center of mass of $S_{1}$ is moving away from $S_{2}$.

Statement (1) concerns the point at which the forces act, so thermodynamic work is relevant. Statement (2) concerns the center of mass, so the center of mass work is relevant.

We have $F_{\text{by 1 on 2}} = -F$ and $F_{\text{by 2 on 1}} = +F$. When considering thermodynamic work, we look at the contact point, whose displacement is $-\Delta x < 0$, and find the following:

  • $W_{F_{\text{by 1 on 2}}} = -F\cdot -\Delta x > 0$, and
  • $W_{F_{\text{by 2 on 1}}} = +F\cdot -\Delta x < 0$.

The fact that $W_{F_{\text{by 1 on 2}}}$ is positive means that $S_{2}$ is gaining overall energy, and the fact that $W_{F_{\text{by 2 on 1}}}$ is negative means that $S_{1}$ is losing overall energy. This makes perfect sense, because $S_{1}$ is losing potential energy to $S_{2}$ (and the remaining energy that stays with $S_{1}$ is converted to kinetic energy).

When considering the center of mass work, we look at the center of masses. The CoM of $S_{1}$ is displaced by $+\Delta x > 0$ and the CoM of $S_{2}$ is displaced by $-\Delta x < 0$. We find the following:

  • $W_{F_{\text{net on 1}}} = +F\cdot +\Delta x > 0$, and
  • $W_{F_{\text{net on 2}}} = -F\cdot -\Delta x > 0$.

The net work for each system is positive. This is exactly what is expected by the work-energy theorem: both objects gain kinetic energy and accordingly the center of mass work for both is positive.

Summary

Returning back to

There is also work done by the object on you, but the issue is, that other object didn't have any potential energy. So how can the other object do work on you, without transferring any energy to you? What is the right way to think about this situation?

We have to clarify what we mean by work.

If by "work" we mean "work due to a contact force," then in the OP scenario, the person jumping off is doing positive work on the other object, and the object is doing negative work on the person, because you must track the point at which the force is applied. Accordingly, the person's total energy decreases and the total energy of the object increases.

If by "work" we mean "net work"/"center of mass work"/"pseudowork", then in the OP scenario there is positive work done on both the person and the object. Accordingly both have an increase in kinetic energy. This of course says nothing about how the total energy is transferred, because the work-energy theorem only deals with changes in kinetic energy only. Thus, there is no issue or contradiction.

Related:

MaximusIdeal
  • 8,868