0

Possible Duplicate:
Why can't a piece of paper (of non-zero thickness) be folded more than "n" times?

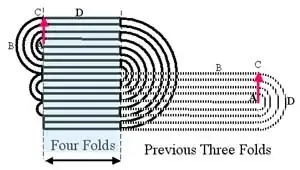
On skeptics.stackexchange, there is a question on the maximum limit on the folds of a paper. The referenced answer said that Britney Gallivan derived an equation to estimate the number of maximum folds possible for a given sheet of paper. The answer justified the 'only'-folding scenario but when the same scenario is changed to folding the paper preceded by tearing the paper off into two equal halves, it fails.

I tried to tear an A4 sheet off in two equal halves and kept on tearing it in two equal halves in alternate directions by first folding the paper and then tearing it. After the 7th tear-off, I found that I could still fold the paper for the 8th time. Applying the same reasoning here, the A4 should fail to fold for the 8th time but it doesn't. Why?

Community
  • 1
Harsh
  • 101

2 Answers2

1

The point about Britney Gallivan's work is that not only do you lose length when folding several sheets, but that this accumulates and she worked out the impact of this accumulated loss. This is illustrated in the Historical Society of Pomona Valley page "Folding Paper in Half 12 Times" linked from the skeptics.se page with this picture

enter image description here

where the length of parallel paper after four folds is substantially less than half that after three folds.

But if you tear the paper after each fold then you do not have this accumulation, so you would naturally expect to be able to fold more times when tearing is allowed. That is what you have confirmed.

Henry
  • 2,008
-2

If you had a sheet of sufficient size and folded in half once again, forty times, how thick would be?

In principle we could think we can do bends over 100 times, however, be surprised that you can not get more than 8 or 9 folds. The record is 12 and this very difficulty!.

It happens that when we fold the paper also doubling its thickness, and thus the folding it difficult to follow.

Depue first folded thickness is doubled, that is,$$ E = 2e $$ Where "E" is the thickness of the folded sheet and e the thickness of the original sheet.

The second fold is the total thickness of $$E '= 2E $$, and the above formula $$E' = 4e $$ or $$E '= 2 * 2e $$ .

Staring into the last sentence we can infer that, for example, the folding number 8 the total thickness will be $$E '= 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * e $$ By multiplying the account found that in only 8 fold increased the total thickness ... .. 256 times !!!!!

jormansandoval
  • 1,546