Definition of spatial and temporal coherence in QM?

Question

It is often said that lasers are spatially and temporally coherent. Is there a simple definition of spatial and temporal coherence in the language of quantum mechanics? More specifically, can these be stated as constraints/measures on a certain degree of freedom of an ensemble of photons?

Answer 1

To talk about lasers specifically we need to discuss the quantization of the electromagnetic field, i.e. quantum field theory (QFT). In order to avoid that subject for the moment and to build intuition I will focus on the far simpler case of the quantum harmonic oscillator (QHO).

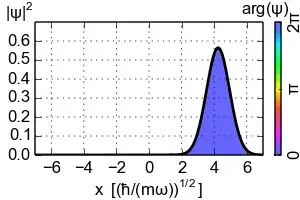
The most intuitive definition is that a coherent state is a state of minimal uncertainty in both position and momentum. Since the uncertainty principal states that $$ \Delta x\Delta p \geq \frac{\hbar}{2}, $$ a state which has minimum uncertainty in both must have $\Delta x = \Delta p =\sqrt{\frac{\hbar}{2}}$. What this means is that we can think of the probability distribution of a coherent state as being centered on a location $x(t)$ and evolving under the Schrödinger equation as a classical particle would in the potential $V(x)$ used to define the Hamiltonian. In the case of the QHO this looks something like:

                                                 

Now, this is all well and good for intuition but we should also ask how one obtains such states mathematically. The answer turns out to be remarkably simple. Recall that the QHO hamiltonian can be written in terms of ladder operators. That is, if we take the Hamiltonian written in terms of the usual position and momentum operators

\begin{equation} \hat{H}=\frac{{\hat p}^2}{2m} + \frac{1}{2} m \omega^2 {\hat x}^2 \ \end{equation}

We can define

\begin{align*} \hat{a} &=\sqrt{m\omega \over 2\hbar} \left(\hat x + {i \over m \omega} \hat p \right) \\ \hat{a}^\dagger &=\sqrt{m\omega \over 2\hbar} \left(\hat x - {i \over m \omega} \hat p \right) \end{align*}

which when inverted to obtain $\hat{x}$ and $\hat{p}$ give \begin{align*} \hat x &= \sqrt{\frac{\hbar}{2 m\omega}}(\hat{a}^\dagger + \hat{a}) \\ \hat p &= i\sqrt{\frac{\hbar m \omega}{2}}(\hat{a}^\dagger - \hat{a}). \end{align*}

When plugged into the hamiltonian for the QHO we obtain a very simple form $$ \hat{H} = \hbar\omega\left(\hat{a}^\dagger \hat{a} + \frac{1}{2}\right). $$

With this form of the hamiltonian one can clearly show what the more complicated description of the QHO energy eigenstates written in terms of Hermite polynomials obscures - they are nice because $\hat{H}|n\rangle = \hbar\omega \left(n + \frac{1}{2}\right)$ and can be thought of as how many units of energy are in the state. In this description, the eigenstates are labeled by an occupation number $n\geq 0$ as $|n\rangle := \frac{1}{\sqrt{n!}} \left(\hat{a}^\dagger\right)^n \left|0\right\rangle$ with the vacuum state $|0\rangle$ defined as the unique state satisfying the property $\hat{a}|0\rangle = 0$.

Now, a question that is not often asked in an undergraduate QM course is what do the eigenstates of the ladder operators themselves look like? In other words, what is a state $|\alpha\rangle$ written in the occupation number basis such that $\hat{a}|\alpha\rangle = \alpha|\alpha\rangle$? Well, it is not too hard to see using the ladder operator commutation relations that $$ |\alpha \rangle :=e^{\alpha {\hat {a}}^{\dagger }-\alpha ^{*}{\hat {a}}}|0\rangle=e^{-{|\alpha |^{2} \over 2}}\sum _{n=0}^{\infty }{\alpha ^{n} \over {\sqrt {n!}}}|n\rangle ,\ \alpha \in\mathbb{C} $$

is such a state. When one examines the probability of finding $n$ units of energy in this states, you get a Poisson distribution over $n$.

So what was the point of this? You can show that a QHO state satisfying $\Delta x = \Delta p =\sqrt{\frac{\hbar}{2}}$ must be an eigenvector of $\hat{a}$ (see this wikipedia section for an explanation of why); so we have found the mathematical description of our coherent states! In fact the gif above which I lifted from the coherent state wikipedia page is the case when $|\alpha|=3$.

Finally, what does any of this have to do with lasers? Well, in a course on QFT you learn that a quantum field can be decomposed into a Fourier expansion of its plane wave modes labeled by their frequency and wavenumber. The Fourier coefficients of the classical field, upon quantization, become an infinite set of ladder operators $\hat{a}^\dagger_\vec{p}$ and $\hat{a}_\vec{p}$ which add and remove particles of momentum $\vec{p}$. Just as we did for the QHO we can create coherent states out of these ladder operators, and they are now thought of as superpositions over field configurations which have minimum uncertainty around a classical field configuration of specific frequency (note momentum and frequency are intrinsically related to one another due to special relativity and QM). So this is why lasers are called coherent states: they are the closest possible quantum mechanical state of the electromagnetic field which behaves like a classical wave of a single frequency.

As an interesting aside, these coherent states in QFT are the real source of the famous wave-particle duality in quantum theory. By taking an appropriate quantum superposition of particle-like states we end up with something very close to a classical wave!

Answer 2

Coherence in quantum optics is usually described in terms of $n$th-order correlation functions describing correlations of expectation values of field observables at $2n$ different locations in space and time, which can be measured by $n$-fold coincidence measurements as explained in The Quantum Theory of Optical Coherence by R. J. Glauber. Coherent states at the $n$th order are those capable of showing constructive or destructive interference at that order.

For a more recent review that describes both single photon and multi photon effects see The spatial behavior of nonclassical light by MI Kolobov.