0

Consider the reduced radial Schrodinger equation:

$$-\frac{1}{2}\frac{\text{d}^2}{\text{d}r^2}\phi(r)+V(r)\phi(r)=E\phi(r).$$

We try to find a bound state (i.e. $\phi(0)=\phi(+\infty)=0$).

Here $V(r)=1/r$ or $1/r^2,1/r^3$ etc.

A numerical approach showed that the energy $E$ tends to zero when $a$ (i.e. the upper bound for $r$, use it to represent $+\infty$ in the numerical method) increases.

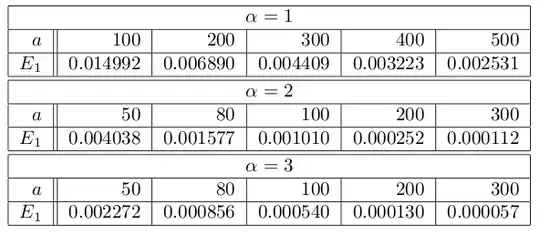
table1

(In this table $V(r)=1/r^{\alpha}$. $E_1$ is the calculated energy.)

My question is, how to explain this result physically?

Is that the real $E$ should be $0$, or allowed $E$s actually are continuous?

I think it is because of the repulsive potential $V(r)$, that $E$ should be $0$.

(P.S. I'm interested in the "ground state", if it exists. My numerical procedure tries to find the minimum energy. )

Community
  • 1
NGY
  • 601

1 Answers1

4

There are no bound states for this potential, for any positive $\alpha$. All energies $E>0$ are allowed, and all of those are unbound states, in which $\phi\sim e^{ikr}$ for large $r$, with $E=k^2/2$.

The easiest way to prove that there are no states with $E<0$ is to show that the expectation values of both kinetic energy and potential energy, $\langle T\rangle$ and $\langle V\rangle$, are positive for any valid wavefunction. For an energy eigenfucntion, $E=\langle E\rangle=\langle T\rangle+\langle V\rangle>0$.

The fact that these aren't bound states -- that is, that they go as $e^{ikr}$ rather than as a decaying function of $r$ at large distances -- is most easily seen from the fact that, at sufficiently large $r$, the potential term is always negligible in comparison to the right-hand side. So at large $r$ we have $-\phi''/2=E\phi$.

Ted Bunn
  • 20,263