It is indeed possible to make experimental realizations which are very close to the ideal infinite quantum well. The cleanest way to do this is using what are known as nanostructures / heterostructures in semiconductor joints, as well as quantum dots and quantum wires.
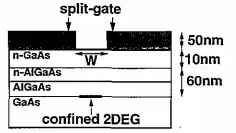
Semiconductor nanostructures work by confining electrons to the interface between layers made of different semiconductors. At the interface between them, the interaction between the different Fermi surfaces can cause a sharp downward spike in the chemical potential. This creates a sharp quantum well in the $z$ direction in which electrons can accumulate, and if you cool the material to liquid helium temperatures they will collect at the well's ground state. This effectively 'freezes out' the motion in that direction, and the result is known as a 2-dimensional electron gas. (The Wikipedia page also has nice explanations.)
A good review of this technology is
The role of surface-gate technology for AlGaAs/GaAs nanostructures. R.P. Taylor. Nanotechnology 5 no. 4, 183 (1994).
The motion of this electron gas in the $x,y$ plane is then further controlled by electrodes on the surface of the device. Using box-like electrodes, you can get the confined electron gas to reproduce at least the first few states of the particle-in-a-box.
Optical emission and Raman scattering in modulation-doped gaAs-AlGaAs quantum wires and dots. P.D. Wang et al. Superlattices and Microstructures 15 no. 1, 23 (1994).
Some other references which look good for this are
Probing Many Body Effects in Semiconductor Nanostructures. Ron M. Potok, PhD thesis. Harvard University, 2006.
and the chapter on nanostructures in
Introduction to Solid State Physics. Charles Kittel, Wiley, 2005; ark:/13960/t4vh6vm9v.
That said, it is hard to get beyond the first few levels of the particle-in-a-box, and there is no real reason to try hard to obtain this. Instead, two-dimensional electron gases offer an amazing laboratory to study a broad range of phenomena encoded by single-particle Schrödinger equations in two dimension. For a nice review of more recent work, including cyclotron orbits and Aharonov-Bohm interferometry, see
Time‐dependent approach to transport and scattering in atomic and mesoscopic physics. Tobias Kramer. AIP Conf. Proc. 1334, 142 (2011), in XL Latin American School of Physics, Mexico City, 26 July–6 August 2010.
