Apart from the possibility that radio transmission will not work, what would happen if someone travelling fast enough relative to another individual to experience significant time dilation made a phone call or a radio transmission? Would one side sound like they are talking really slowly to the other?(assuming its an analog radio and doppler shift is accounted for so that they can in fact communicate)
1 Answers
Your experiment is a bit more complicated than you might think because there are two effects at play. I would guess you're really interested in the effect of time dilation, but there is also a slowing because the distance between you and the moving person is increasing with time.
Suppose I'm counting at one number per second, and I count "one" as I pass you at velocity $v$. Ignore time dilation for now. When I say "two" I'll be at a distance $d = v$. It takes a time $d/c = v/c$ for you to hear me say "two" over the radio, so the total time you measure between me saying "one" and me saying "two" is:
$$ t' = 1 + \frac{v}{c} $$
So even ignoring the effects of time dilation you're going to hear me speaking more slowly. Actually this is just the Doppler effect - it's exactly the same reason that the frequency of the signal from my phone is reduced when you receive it. You say in a comment:
If Doppler shift were accounted for, wouldn't that undo all effects?
But how do you plan to account for the Doppler shift? You can tune your radio receiver so it matches the reduced frequency of the signal from my phone, but whatever you do you'll still hear me talking more slowly.
Can I suggest a modification to your experiment that gets round this problem? Suppose I'm sitting in a centrifuge whirling around you at velocity $v$:
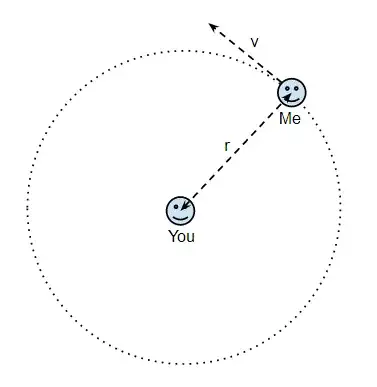
In this case the distance, $r$, between us doesn't change so there is no Doppler effect to confuse our measurements and any slowdown you can here must be due solely to time dilation. You might think the time dilation must be harder to calculate with this geometry, but actually with some effort you can show that the time dilation between us is exactly the same as if I was moving in a straight line at velocity $v$. If you're interested I prove this in my answer to Is gravitational time dilation different from other forms of time dilation?.
So your question becomes What happens if someone circling me at just under the speed of light makes a telephone call? and the answer is actually quite boring: you would just hear them talking more slowly by a factor of $\gamma$, where $\gamma$ is given by the usual special relativity formula:
$$ \gamma = \frac{1}{\sqrt{1 - \tfrac{v^2}{c^2}}} $$
Note that the carrier frequency of my phone will be reduced by the same ratio so you'll need to retune your radio receiver to receive the signal from my phone just like in your original experiment.
- 367,598