I was recently calculating the one loop correction for the propagator of a gauge boson,
$\hspace{5cm}$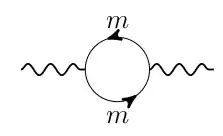
I assumed arbitrary left and right couplings, $ g _L $ and $ g _R $. I found that the one loop correction was, \begin{equation} = \frac{ - 4i }{ ( 4\pi ) ^{ d / 2}} \int dx \frac{ \Gamma ( 2 - d / 2 ) }{ \Delta ^{ 2 - d /2 }} \left[ ( g _L ^2 + g _R ^2 ) x ( 1 - x ) \left( g _{ \mu \nu } - \frac{ p _\mu p _\nu }{ p ^2 } \right) + g _{ \mu \nu } ( g _L ^2 - g _R ^2 ) m ^2 \right] \end{equation} Now we also know that for a $ U(1) $ invariant theory we should have the Ward identity and hence this one loop correction would be of the form, \begin{equation} \Pi _{ \mu \nu } = \Pi ( p ^2 ) \left( g _{ \mu \nu } - \frac{ p _\mu p _\nu }{ p ^2 } \right) \end{equation} So it appears that in order for this propagator to arise from a $U(1)$ invariant theory, we must have $ g _L = g _R $ (unless I made a mistake). I found this very strange. Is it not possible to gauge a $ U(1) _L $ symmetry and if so why?
As a working example I invented the theory below which seems like it could be gauged: \begin{equation} {\cal L} = i \psi ^\dagger \bar{\sigma} ^\mu \partial _\mu \psi + i \chi \sigma ^\mu \partial _\mu \chi + \phi ^0 \chi \chi + \phi ^{+ + } \psi \psi + \phi \mbox{ terms} \end{equation} where $ \psi $ is a left chiral spinor and $ \chi $ is a right chiral spinor. The particles transform under the symmetry as, \begin{equation} \psi \rightarrow e ^{ i \alpha } \quad \chi \rightarrow \chi \quad \phi ^0 \rightarrow \phi ^0 \quad \phi ^{ + + } \rightarrow e ^{ - 2i \alpha } \phi ^{ + + } \end{equation} This seems like a perfectly fine theory, whose symmetry can be gauged but if my conclusion above is correct for some reason I shouldn't be able to gauge this $ U(1 ) _L $ symmetry. Did I make a mistake or is there some deep reason this can't be done?