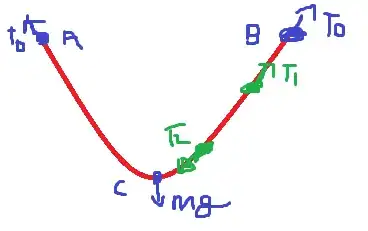
You can only do the balance of forces between spatially separate points only if you know the slope of the rope at each point, and the weight of the rope between the points only.
To get there you use a small section to derive the differential equations and then integrate over the range of $x$ values you want.
Given a small section of rope spanning the horizontal distance ${\rm d}x$ then the tangential distance is ${\rm d}s = \sqrt{ {\rm d}x^2 + {\rm d}y^2 }$ which leads to the expression ${\rm d} s = \sqrt{1+y'^2}\, {\rm d}x$ where $y'=\tan \theta$ is the slope.
The total weight of the rope in this section is thus ${\rm d}w = \mu g\, {\rm d} s$ where $\mu$ is the linear density of the rope $\mu = \rho A = \frac{m}{\ell}$ with $\rho$ mass density, $A$ the cross sectional area, $m$ the total hanging mass and $\ell$ the total hanging length.
At each point if we split the tangential tension $T$ into horizontal part $H$ and vertical part $V$ such that $\tan \theta = \frac{V}{H}$ and $T=\sqrt{H^2+V^2}$
This leads to the following equations
$$ \begin{align} \frac{{\rm d}H}{{\rm d}x} &= 0 \\ H \frac{{\rm d}^2 y}{{\rm d}x^2} &= \mu g \frac{{\rm d}s}{{\rm d}x} = \mu g \sqrt{1+\left(\frac{{\rm d}y}{{\rm d}x}\right)^2} \end{align} $$
In the end you get an equation for the shape of the rope $y(x)$ called a catenary. To get the balance of forces between points (1) and (2) above you have
$$ \begin{align} -T_1 \cos \theta_1 + T_2 \cos \theta_2 &= 0 \\
-T_1 \sin \theta_1 + T_2 \sin \theta_2 &= \mu g \int_{x_1}^{x_2} \sqrt{1+\left(\frac{{\rm d}y}{{\rm d}x}\right)^2} {\rm d}x \\
\tan \theta_1 &= \frac{{\rm d}y}{{\rm d}x} \vert_{x=x_1} \\
\tan \theta_2 &= \frac{{\rm d}y}{{\rm d}x} \vert_{x=x_2} \\
T_1 &= H \sqrt{1+\left(\frac{{\rm d}y}{{\rm d}x}\right)^2} \vert{x=x_1} \\
T_2 &= H \sqrt{1+\left(\frac{{\rm d}y}{{\rm d}x}\right)^2} \vert{x=x_2}
\end{align}$$
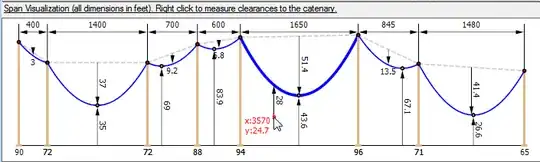
PS. I know all this works because I used the above to create a catenary solver: