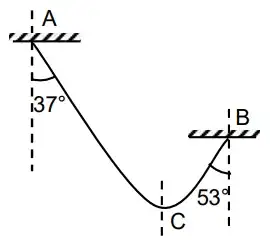
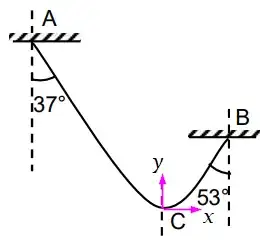
A uniform massive string of mass $m$ and length $l$ is fixed between two rigid supports. Angles made by the tangents on the string at points of suspension are shown in the figure. The point C is the lowermost point of the string. Then choose the correct statements: $\left(\text{Use} \cos(37^{\circ})=\dfrac45\right)$
(A) Length of the string left of the point C is $\dfrac{16l}{25}$
(B)Tension in the string at point C is $\dfrac{12mg}{5}$
(C)Radius of curvature of the string at point C is $\dfrac{12l}{25}$
(D)Tension in the string at point B is $\dfrac{3mg}{5}$
I found the tensions in the left (call it $T_1$) and right parts (call it $T_2$) by simply using the equations:
$\begin{align}T_1 &\cos(37^{\circ}) + T_2\cos(53^{\circ})=mg \hspace{50pt} \text{(for vertical equilibroum)} \\ &T_1\sin(37^{\circ})=T_2\sin(53^{\circ}) \hspace{50pt} \text{(for horizontal equilibrium)}\end{align}$
So that $T_1=\dfrac{4mg}{5}$ and $T_2=\dfrac{3mg}{5}$ and that indeed is the correct answer.
For finding the radius of curvature and length, I need to form a differential equation, but that is where I am stuck. Ideally, the heights of the strings are equal in a catenary and one could use the equation $y=a\cosh\left(\dfrac{x}{a}\right)$, but how do we solve this case?