Why is the Schwarzschild radius the radius of an event horizon?

Question

I've been searching the web and many references without much success. My question is how do we know that, in the Schwarzschild black hole solution, the surface with coordinate $r=2M$ (in the geometric unit system) defines an event horizon, in the sense that every timelike or null curve that crosses that surface - to the interior - will end up in the singularity at $r=0$?

Answer 1

Remember that the definition of an event horizon is "the past boundary of future null infinity". What this means, in common language is -- take all of the light rays that escape to infinity. Then, find the one that just barely doesn't make it back out to infinity. The surface formed by these light rays is the event horizon.

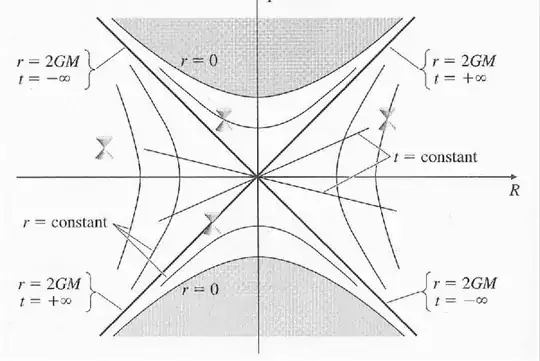
Now, look at a the Kruskal diagram of the Schwarzschild spacetime (this is the Schwarzschild spacetime written in coordinates that don't go singular at the horizon).

The solid black diagonal lines intersecting the middle correspond to $r = 2M$. They are obviously the asymptotes of the curves at the top and the bottom representing $r=0$, so $r=2M$ is the event horizon of Schwarzschild spacetime. (well, technically, the upper triangle formed by the $r=2M$ surfaces is the "future" event horizon of the spacetime, and the bottom triangle is the "past" event horizon of the white hole, but you probably don't care about pedantry like that.)

Answer 2

In Schwarzschild coordinates, if you look at the $g_{tt}$ and $g_{rr}$ parts fo the metric, they flip signs at $r=2M$. Therefore for $r<2M$ the $r$ direction is timelike and the $t$ direction is spacelike. The future-timelike light cone of any event inside the horizon points toward smaller values of $r$.

Answer 3

This is what Penrose and Hawking proved with the Penrose-Hawking singularity theorems. Specifically, and I quote from the linked article:

Penrose concluded that whenever there is a sphere where all the outgoing (and ingoing) light rays are initially converging, the boundary of the future of that region will end after a finite extension, because all the null geodesics will converge. This is significant, because the outgoing light rays for any sphere inside the horizon of a black hole solution are all converging

This proves any world line crossing the event horizon must end at the singularity.

Answer 4

I'll attempt an answer from a different perspective from the rest.

The Schwarzschild solution is the vacuum solution for a static, spherically symmetric spacetime.

The Schwarzschild coordinates are 'nice' for the solution for at least two reasons:

(1) the line element far away from the spatial origin, in these coordinates, approaches the line element of flat spacetime in spherical coordinates

(2) the surface area of a sphere at radial coordinate $r$ is $4\pi r^2$

However, it turns out that the coordinates do not cover the entire spacetime since the requirement that the spacetime is static cannot be satisfied for the entire spacetime.

This is essentially the reason that there is a coordinate singularity at $r = 2M$, the boundary between the exterior region, where the geometry is static, and interior region where the geometry is dynamic.

There is a coordinate transformation from the Schwarzschild $r, t$ coordinates to the Kruskal–Szekeres $U, V$ coordinates as follows:

For the exterior region,

$$V = \left(\frac{r}{2M} - 1\right)^{1/2}e^{r/4M}\sinh\left(\frac{t}{4M}\right)$$

$$U = \left(\frac{r}{2M} - 1\right)^{1/2}e^{r/4M}\cosh\left(\frac{t}{4M}\right)$$

and, for the interior region,

$$V = \left(1 - \frac{r}{2M}\right)^{1/2}e^{r/4M}\cosh\left(\frac{t}{4M}\right)$$

$$U = \left(1 - \frac{r}{2M}\right)^{1/2}e^{r/4M}\sinh\left(\frac{t}{4M}\right)$$

In these coordinates, the line element is

$$ds^{2} = \frac{32M^3}{r}e^{-r/2M}(-dV^2 + dU^2)$$

where $r$ is implicitly defined by

$$V^2 - U^2 = \left(1-\frac{r}{2M}\right)e^{r/2M}$$

Thus, in these coordinates, there is no coordinate singularity at $r=2M$. Indeed, we have

$$U^2 = V^2$$

for $$r = 2M$$

But, from the line element, we see that when

$$dU = \pm dV$$

the interval is null (light-like) thus, world lines with $U^2 = V^2$ are light-like; the surface $r=2M$ is a null surface, i.e., lies on a lightcone. Only massless entities can remain at $r=2M$.

There is a true spacetime singularity for $r=0$. In the $U,V$ diagram, $r=0$ corresponds to the hyperbola

$$V^2 - U^2 = 1$$

The asymptotes are the $r=2M$ light-cone. It immediately follows that the singularity is in the future of any world-line in the interior region.

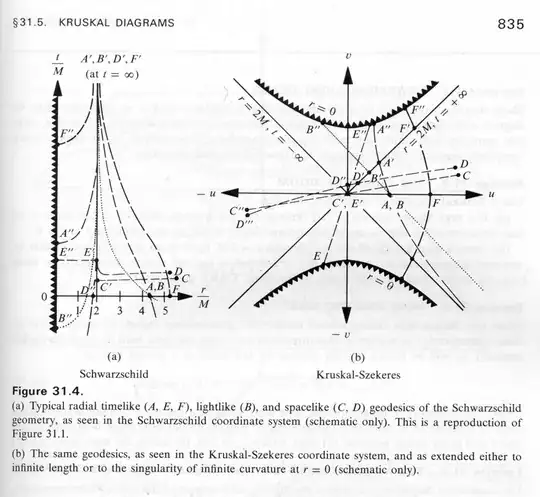
Below is an image, from MTW's "Gravitation", of a comparison of various geodesics of the Schwarzschild spacetime in Schwarzschild coordinates and Kruskal–Szekeres coordinates