Why is the pressure inside a soap bubble higher than outside?

Question

Apparently, the air inside a soap bubble is under higher pressure than the surrounding air. This is for instance apparent in the sound bubbles make when they burst. Why is the pressure inside the bubble higher in the first place?

Answer 1

I drew an image to illustrate the forces at play.

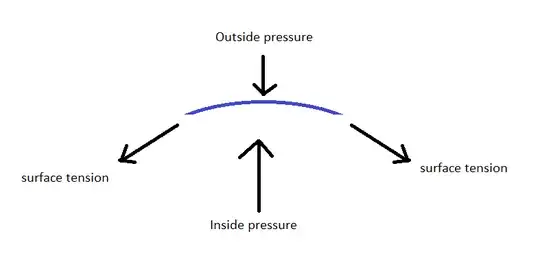
For any curved surface of the bubble, the tension pulls parallel to the surface. These forces mostly cancel out, but create a net force inward. This compresses the gas inside the bubble, until the pressure inside is large enough to counteract both the outside pressure, as well as this additional force from the surface tension.

Answer 2

The increased pressure is caused by the surface tension between the soap and the surrounding air. This can be seen by a simple equilibrium energy argument. The total energy of the system reads $$ E = E_i + E_o + E_s \;, $$ where $E_i$ is the energy associated with the air inside the bubble, $E_s$ is the interfacial energy, and $E_o$ denotes the energy associated with the air outside of the bubble. Importantly, the contribution of the surface energy is given by $E_s = 2 \gamma A$, where $\gamma$ is the surface tension and $A$ is the surface area of the bubble. The factor of 2 emerges, since there are actually two interfaces (one facing the inside of the soap bubble and one facing the outside).

In equilibrium, the total energy will be minimal. We thus analyze the total differential of the energy. Here, the differentials of the partial energies of the air can be approximated by the ideal gas law, which yields $dE_i = -p_i dV_i$ and $dE_o = -p_o dV_o$. Next, we have to discuss the degrees of freedom of the system. Generally, the soap bubble wants to keep its spherical shape to minimize the surface area (and thus the surface energy $E_s$) at a given volume. This leaves us with a single parameter, the radius $R$ of the bubble, which can be varied in any process. The volume differentials then become $dV_1 = 4\pi R^2 dR$ and $dV_2 = -4\pi R^2 dR$. Additionally, the surface area changes by $dA = 8\pi R dR$. The differential of the surface energy thus reads $dE_s = 2\gamma 8\pi R dR$, provided that the surface tension stays constant.

Now we got everything and can express the differential of the total energy as $$ dE = -p_i 4 \pi R^2 dR + p_o 4\pi R^2 dR + 2\gamma 8\pi R dR \;. $$ Dividing by $4\pi R^2$ and noting that $dE/dR$ vanishes in equilibrium, we thus arrive at $$ p_i - p_o = \frac{4\gamma}{R} \;. $$ This expression shows that the pressure inside the bubble is large than outside. The pressure difference is two times the Laplace pressure $2\gamma/R$.

Answer 3

It is like a balloon. The pressures of the inner and outer air tend to equilibrate, creating a force over the balloon surface from the higher pressure to the lower one, trying to make them equal (the force goes from inside to outside, when you inflate it, from outside to inside when you deflate it). That's why it changes its size, because the gas pressures tend to be the same. At the other hand, the elastic material of the balloon when it is inflated tries to return to its resting state (deflated), so it creates an inward force compressing the inner air. The balloon reaches its balance (it gets inflated at a certain level) when these two forces are equal. That means that the inner air will always be at a higher pressure than the outer air, being this difference related to the balloon material elasticity (the more the material resistance to inflate/deform is, the more the pressure difference will be). In a bubble this resistance to inflate is due to the surface tension (a contractive force that always tries to leave a liquid surface at its minimum; that's why bubbles and droplets are spherical). (I'm not a native english speaker, please be comprehensive with expression)

Answer 4

The simple answer to "why is the pressure inside a soap bubble higher than outside," is that a higher pressure than the local atmosphere is required to make the bubble in the first place! This requirement comes from the need to counterbalance the surface tension force.

For stable conditions, $$F_i = F_o + F_s $$ Where $F_i$ is the force due to inside pressure, $F_o$ is the force due to outside pressure, and $F_s$ is the force due to surface tension.