Why is it that when you first fill up a balloon, it's hard to get air through, but after inflating it a bit, it becomes much easier to further inflate the balloon?
12 Answers
I think that most of the answers here are incorrect since it has nothing to do with decreasing resistance of rubber. In fact, the force required to stretch the balloon increases, not decreases while inflating. It's similar to stretching a string, ie. the reaction force is proportional to the increase in length of the string - this is why there is a point when you can no longer stretch a chest expander.
The real reason that initially it's hard to inflate the balloon is that in the beginning, ie. with the first blow, you increase the total surface of the balloon significantly, thus the force (pressure on the surface) increases also significantly. With each subsequent blow, the increase of the total surface is smaller and so is the increase of force. This is the result of two facts:
- constant increase of volume with each blow
- volume of the balloon is proportional to the cube of radius while surface of the balloon is proportional to the square of the radius
For a sphere you have:
$$ A={4}\pi R^2 \\ V={4\over3}\pi R^3 $$ The equations says that the amount of work required to increase the volume of the balloon by one unit is smaller if the balloon is already inflated.
- 954
Take a strip of balloon rubber and pull it. It will get harder the more you pull. So why is it that inflating the balloon gets easier (at least long before the breaking point)?
The balloon starts with very high curvature, so the air pressure is distorting each spot on its surface a lot relative to its 1cm neighbors for example. All the rubber's tension pulls inwards at a relatively sharp angle. With a larger balloon, this angle becomes flatter.
Imagine you have a thread attached to the wall. You hang a weight from the centre of the thread and pull the other end away. Now pulling gets harder and harder as the angle between the ends of your thread gets wider. The impact of the weight is getting bigger, even though the weight is not changing. Conversely, if you pull with a consistent force on your thread, you need a much bigger weight to produce a sharp angle than to produce a wide angle.
This effect is largely overcompensating the actually increasing tension in the rubber.
Try it out with http://www.calculatoredge.com/calc/sphere.htm It's not perfect, mainly as it doesn't provide reasonable numbers to start with but find some and then change pressure and volume to see the effects on the stress. Twice the radius would mean twice the stress, so conversely you need half the pressure if the stress staid the same, to inflate a twice as big balloon.
- 115
- 6
- 121
When in doubt, use mathematics.
Imagine the balloon as a sphere (close enough for this answer) of initial radius $r_0$ and thickness $t$. Let's inflate it just a little bit from the uninflated state (to radius $r_0 + \Delta r$). Now we can take a look at what happens by taking a cut through the equator of the sphere. The total circumference at the equator is $2\pi r$; with the thickness $t$ the area of rubber we're working against is $2\pi r t$. Stretching the balloon's radius by $\Delta r$ increases the circumference by a fraction of $\frac{\Delta r}{r}$ - that is the strain. Now if we accept that rubber is a perfectly elastic material (constant Young's modulus E), then the force we need to exert is $$\begin{align}F &= E\cdot2 \pi \cdot r \cdot t \cdot \frac{\Delta r}{r}\\ &=2\pi \cdot E \cdot t \cdot \Delta r\\ \end{align}$$
so force is independent of radius - although it does depend on the degree of stretching ($\Delta r$).
Now the force on the rubber is generated by the pressure in the balloon divided by the area at the equator:
$$\begin{align} F &= P A\\ &= \pi r^2P\\ \end{align}$$
Combining these two, you get
$$P = \frac{2 \cdot E \cdot t \cdot \Delta r}{r^2}$$
Because there is an $r^2$ term in the denominator, this shows that pressure will be less when the balloon gets bigger - in other words, blowing a balloon is initially harder, as is the general experience.
But wait - there's more. The thickness of the balloon becomes less as the balloon stretches - for a sphere this is a slightly complex quantity involving the Poisson ratio of the material. But the point is that $t$ will become smaller as $r$ gets larger: this will make pressure drop even faster with radius.
Finally, the modulus of elasticity isn't quite constant - in particular, when rubber is stretched beyond a certain point it becomes much stiffer. This is the reason that the balloon, having initially become easier to inflate, finally become quite hard - and continuing to blow it further may make it pop.
- 119,981
Like Dev said above, the material your typical round balloon is made from has a non-linear stress strain curve. When just starting to inflate it is fairly stiff, but then as it starts to blow up the stiffness goes down somewhat until it approaches its maximum size. We measured this in my undergraduate advanced lab class, and while I don't have the data handy there's a web site that shows a stress-strain curve for a balloon.
Edit: Swapped out the original link, unclear if the page had malicious content or not? I had no warnings in recent versions of firefox and chrome, but better safe than sorry.
The volume of a balloon grows linear, while the surface (which you actually stretch) doesn't. So although you're blowing the same amount of air into a balloon, you don't stretch the surface as much as in the beginning.
- 269
Let us first summarize what do we actually experience when inflating the balloon. For the very first bit of volume, we have to exert a lot of energy. Or alternatively, we have to apply a lot of pressure coming from our lungs because for the change of energy $\delta E$, change of volume $\delta V$ and extra pressure $\Delta P$ (that is the difference between the actual and the atmospheric), we have roughly
$$\frac{\delta E}{\delta V} \approx \Delta P$$
ARM, golem and John Bentlin pointed out effects that surely cause a balloon to be more difficult to inflate when it is less inflated rather than a lot. However, it is not entirely clear which of the effects plays the major role in this case.
The effect of an "S-curve" in the tensile response of the balloon is nevertheless significant only around the tensile pressure that is at the pressure where we reach the tip of the S-curve. The tensile pressure of rubber is typically around $10-15 MPa$. So we can ask whether by linear stretching in a typical balloon, we reach the tensile pressure in the first blow or not. Once we do, we throw away the model and say afterwards it is much easier to stretch since now the rubber is "over-stretched".
For the pressure inside a spherical volume of diameter r held by a membrane with surface tension $\sigma$, there is a law called the Laplace law and it reads: $$\Delta P = \frac{2 \sigma}{r}$$ The law can be derived by differential calculus and energy variations due to surface growth and volume growth as slightly touched upon by user golem.
For rubber we have a Young's modulus around $E_Y = 0,01-0,1 GPa$. The membrane surface energy can be again by energy considerations derived as
$$\sigma = E_y d$$,
where $d$ is the thickness of the ball wall. However $d$ gets spread out with growing surface, that is as $r^2$. Without further hesitation we can just write an approximate expresion $$d = d_0 \left(\frac{r_0}{r}\right)^2$$
Where $d_0$ and $r_0$ are the initial thickness and density. When we put all the formulas together, we get $$ \Delta P = \frac{2 E_Y d_0}{r} \left(\frac{r_0}{r}\right)^2 $$.
So you can see that the pressure is dropping for higher $r$ as $r^{-3}$. The only chance the S-curve would play a role is if we were close to the tip even for initial values of thickness and $r$. By putting a small $r_0=1cm$, $d_0=1mm$ and $E_Y = 0.1 GPa$, we get an initial pressure of $$\Delta P = 20 kPa$$,
which is by all means less than $15 MPa$, so the S-curve will for sure play no role in the first blow.
To conclude, the pressure is highest for the first blow because both the rubber gets spread out and a larger surface requires less of an investment of energy to contain more volume.
The effects of pre-spreading your balloon just give you a larger $r_0$ and the balloon eventually breaks only because the wall gets too thin and small imperfections cause it to break down even for the very small pressure.
- 21,331
The material of an unstretched baloon does resist stretching; this can largly be overcome by manually pre-stretching it (something I learned from my mom when I was about 5 years old). The other thing I'd consider (and that I don't see mentioned so far) is the cumulitive force exerted on the inner surface of the baloon as it's inflated, calculated by Pressure x Area. Example: a 2" diameter round baloon has in surface area of about 50 sq in. at 2 pounds sq in, that's 100 pounds of force total. At 4" diameter, it has about 200 sq in; at the same 2 pounds per sq in, that's now 400 pounds of force total. The difference in the force is the square of the change in diameter.
- 21
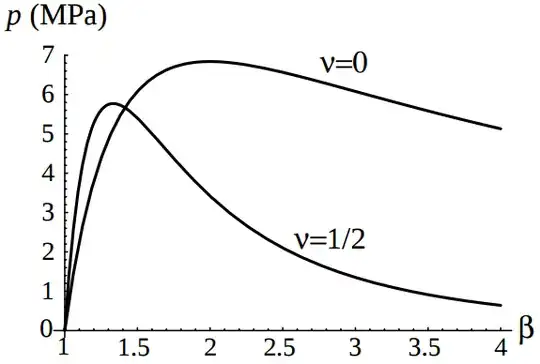
The pressure curve for a rubber balloon
, summarized in the Wikipedia article Two-balloon experiment, derives the pressure using a theoretical stress equation based on the thermodynamic theory of elasticity for an ideal rubber. They find the approximate formula
$$P= \frac{C}{r_0^2 r}\left[1 - \left(\frac{r_0}{r}\right)^6\right]$$
where $r_0$ is the balloon's uninflated radius.
This lecture uses the "two-dimensional, plane stress generalized Hooke’s law with respect to the Eulerian strain measure" (which they call a a very rough approximation) to derive a curve ($\nu = 1/2$ for incompressible).
Both derivations take into account the thinning of the (assumed incompressible) rubber as the membrane stretches.
- 2,371
Because the rubber is thicker initially. Thick rubber is harder to stretch than thin rubber, in proportion to its thickness. And the thickness of the rubber in a balloon is inversely proportional to its surface area.
- 721
The elastic nature of rubber is varying on pressure/temperature inversely, which makes it harder when cool and softer when applied pressure.
So to inflate a balloon in a normal condition we need to put more pressure initially. As when it expands, the pressure inside increases which reduces the elasticity of rubber making it easier to blow later on.
The Elasticity of a material is defined as the tendency of solid material to return to their original shape after being deformed.
We have noticed that when balloon bursts , its pieces becomes cool.This is the reverse effect as when the pressure inside reduces on a sudden it absorbs the room temperature and retains its elasticity.
- 1
Actually it depends on the material of balloon. If the balloon is made of less elastic material then it will become even more difficult to blow it even after little inflation cause it will reach its elasticity limit very early and this might not be true in case of more elastic balloons.
- 1
Intuitively, you can think of it this way:
Pressure is measured as Force / Area, e.g. Pounds per Square Inch (PSI), or Newtons per Square Meter (Pascals). Initially, the surface area inside the deflated balloon is small, meaning more pressure will be required to inflate it. Once you begin inflating the balloon, the surface area inside grows larger and larger. This means that less pressure will be required to inflate it, even though the balloon is resisting with more force as it is stretched.
- 101