Short answer: Your professor is correct.
Long answer: Remember that $\Delta G = G_\text{mixed} - G_\text{unmixed}$. You are correct in saying that for any composition which has $\Delta G < 0$, it is the mixed state that is favorable. However, here mixed does not mean randomly mixed, but rather it is a system where the two components interact, whereas in the unmixed state the components A and B are kept in separate containers. Where $\Delta G < 0$, the container containing both A and B has a lower free energy than the two separated systems.
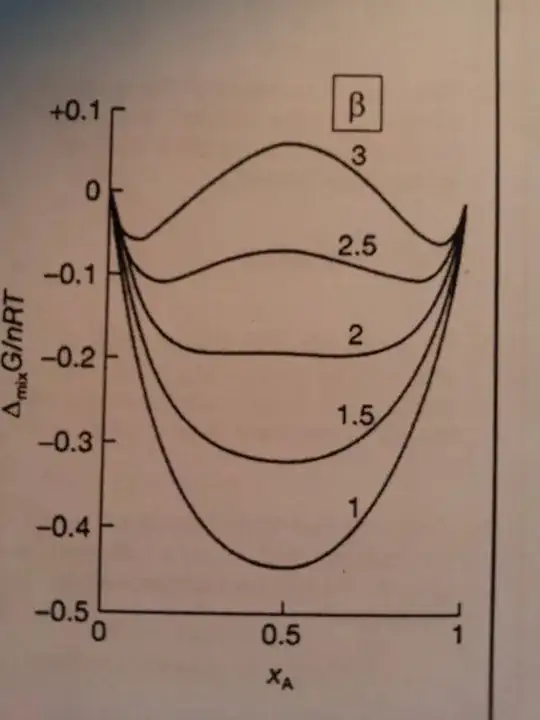
Now take $\beta = 2.5$. No matter what the fraction of A in the mixed container, the mixed system always has a lower free energy than the container containing only A. Imagine that you pour in 50% A and 50% B and mix them. If you kept mixing the container, you would indeed get the free energy at the middle of your graph. If you stopped actively mixing, though, more interesting things would happen: Phase separation. There would be phase X, which is 80% A and 20% B and phase Y, which is 20% A and 80% B (the two minimas in the graph). Neither phase is pure (100% A, say), mind you.
Why should this happen? Imagine your system has 50% phase X and 50% phase Y. Both phase X and phase Y have a free energy lower than that of the phase made up of 50% A and 50% B. If we assume that phase X and phase Y do not interact with each other directly*, then clearly the combination of 50% phase X and 50% phase B has a lower free energy than the system 50% A and 50% B.
For a more general case, there was a recent question (discussion still ongoing) here.
* In actuality, they do, and this is called surface tension (or line tension if you have a 2D system). However, taking the thermodynamic limit this energy does not grow as fast as the system (a surface grows $a^2$ whereas the volume goes like $a^3$), and thus can usually be disregarded in the phase diagram.